Zu den besonderen Dreiecken zählen insbesondere das rechtwinklige und das gleichseitige. Schon Euklid hat eine Konstruktionsvorschrift für rechtwinklige Dreiecke mit ganzzahligen Seitenlängen hergeleitet. Dem ist nicht viel hinzuzufügen – außer man knüpft weitere Bedingungen an diese sogenannten pythagoreischen Dreiecke.
Gleichseitige Dreiecke mit ganzzahligen Seitenlängen gibt es selbstverständlich zu jeder natürlichen Zahl. Deshalb ergänzen wir die Bedingungen und stellen die Frage:
Welche ganzzahlige Seitenlänge muss ein gleichseitiges Dreieck ABC haben, damit ein Punkt D auf der Seite \( \overline{AB} \) diese in zwei Abschnitte mit ganzzahliger Länge teilt und außerdem auch \( \overline{CD} \) eine ganzzahlige Länge hat?
Dass mindestens ein solches Dreieck existiert, wird für ein gleichseitiges Dreieck der Seitenlänge 8 in folgender Skizze belegt:
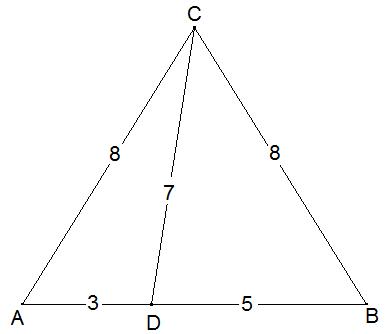
Die beiden Dreiecke ADC und DBC haben ganzzahlige Seitenlängen und jeweils einen Winkel der Größe 60°. Die Zahlentripel (3,7,8) und (5,7,8) heißen in der einschlägigen Literatur (in Anlehnung an pythagoreische Tripel) 60°-Tripel. Damit beginnt unsere Suche nach Antworten auf die eingangs gestellte Frage mit der Suche nach 60°-Tripeln.
Bezeichnen wir die Seitenlänge eines gleichseitigen Dreiecks ABC mit c , die Längen von \( \overline{AD} \) und \( \overline{CD} \) mit a und b, so muss nach dem Kosinussatz gelten
c2=a2+b2-2ab·cos(60°)
und wegen cos(60°)=1/2
(*) c2=a2+b2-ab.
Die Frage nach ganzzahligen Lösungen der Gleichung (*) führt direkt zu Euklids Methode zur Konstruktion pythagoreischer Tripel:
Gleichung (*) wird durch c2 dividiert:
1=(\( \frac{a}{c} \) )2+(\( \frac{b}{c} \) )2-\( \frac{a}{c} \) ∙\( \frac{b}{c} \) . Hier setzten wir frei nach Euklid \( \frac{a}{c} \) =x und \( \frac{b}{c} \) =y und erhalten
(**) 1=x2+y2-xy.
Weiter frei nach Euklid schneiden wir diese Ellipse mit der Geraden
y=\( \frac{n}{m} \) (x+1) mit natürlichen Zahlen m und n, (m>n) so erhalten wir die Schnittpunkte A(-1|0) und B((\( \frac{m^2-n^2}{m^2-mn+n^2} \) |\( \frac{2mn-n^2}{m^2-mn+n^2} \) )). Wegen \( \frac{a}{c} \) =x und \( \frac{b}{c} \) =y ist dann
a=m2-n2
b=2mn – n2
c=m2-mn+n2.
Für m>n sind dies genau die natürlichen Lösungen von Gleichung (*). Für m=3 und n=1 erhalten wir das 60°-Tripel (5|7|8), das wir bereits kennen. Das Dreieck mit den Seitenlängen a=5,b=7 und c=8 lässt sich durch ein Dreieck mit den Seitenlänge d=3, e=7 und f=8 zu einem gleichseitigen Dreieck ergänzen (siehe oben).
Für m=2 und n=1 erhält man das Tripel (3,3,3) das bereits ein vollständiges gleichseitiges Dreieck ist und daher in unserem Zusammenhang ausscheidet. Eine Tabelle für m=3, 4, 5, 6, 7 und n=1, 2, 3, 3, 4, 5 sieht so aus:
n=→
m=↓
| 1
| 2
| 3
| 4
| 5
|
3
| (8,5,7)
| (5,8,7)
|
|
|
|
4
| (15,7,13)
| (12,12,12)
| (7,15,13)
|
|
|
5
| (24,9,21)
| (21,16,19)
| (16,21,19)
| (9,24,21)
|
|
6
| (35,11,31)
| (32,20,28)
| (27,27,27)
| (20,32,28)
| (11,35,31)
|
7
| (48,13,43)
| (45,24,39)
| (40,33,37)
| (33,40,37)
| (24,45,39)
|
Die leeren Felder enthielten nicht ausschließlich positive Zahlen und schieden ebenfalls aus. Schreiben wir aus jedem hier relevanten Tripel die größte Zahl der Größe nach nieder, so erhalten wir: 8, 15, 21, 24, 32, 35, 40, 45, 48,… Dies sind mögliche Seitenlängen zur eingangs gestellten Frage. Da für natürliche Zahlen k auch das k-fache der genannten Zahlen die eingangs gestellte Frage beantwortet, lautet der Anfang der Folge 8, 15, 16, 21, 24, 32, 30, 35, 40, 42, 45, 48,…
Im Internet gibt es in der Online Encyclopedia of Integer Sequences – kurz OEIS – eine Sammlung natürlicher Zahlenfolgen. Zur Folge 8, 15, 16, 21, 24, 30, 32, 35, 40, 42, 45, 48,… wird man unter dem Link, https://oeis.org/?language=german fündig.
Gehen wir nun der Vermutung nach, es gäbe ein einfacheres Konstruktionsprinzip für diese Folge, als das hier entwickelte.
Dafür formen wir die ersten Elemente der Folge ohne Verdopplungen 8, 15, 21, 24, 32, 35, 40, 45, 48,… etwas um:
8=32-12
15=42-12
21=52-22
24=52-12
32=62-22
35=52-12
40=72-32
45=72-22
48=72-12
Jedes Folgenglied ist offensichtlich die Differenz zweier Quadratzahlen s2 und r2, wobei gelten muss: r≤(s-1)/2. Außerdem sind, wie gesagt, auch die natürlichen Vielfachen dieser Glieder in die Folge einzufügen.