Schnittwinkel einer Parabel und einer Normalen

Question

Ich habe die Parabel P Ξ y = x² - 4x + 3 gegeben.

Die errechnete Tangente (T) ist y = x - 3,25; der Berührpunkt B₁ (2,5|-0,75)

Die errechnete Normale (N) ist y = -x + 1,75; N schneidet P bei (0,5|1,25) und (2,5|-0,75)

 

Die zu beantwortende Frage wäre, wie berechne ich den Schnittwinkel von N und P bei Punkt (0,5|1,25). Wir haben bislang noch nicht über Ableitungen gesprochen, obwohl ich stark vermute, dass ich sie hierzu benötige.

 

Answer 1

Eine Möglichkeit OHNE ABLEITUNG wäre folgende Berechnung.

Dazu wird die Tangente ermittelt, die die Parabel bei Punkt (0,5|1,25) berührt.

Ausgangsfunktionen:

T Ξ y = m * x + b (m und b der Tangente sind nicht bekannt)

P Ξ y = x² - 4x + 3

Gleichsetzen:

x² - 4x + 3 = m * x + b

x² - 4x - mx + 3 - b = 0

x² - (4 + m)x + (3 - b) = 0

pq-Formel anwenden:

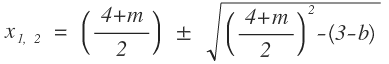
Da es sich um eine Tangente mit einem Berührpunkt (0,5|1,25) handelt, kann jetzt x_{1, 2} = 0,5 gesetzt werden. Wir wissen, dass die Diskriminante der quadratischen Gleichung D = 0 ergeben muss.

Somit haben wir:

0,5 = (4 + m) / 2

m = -3

Einsetzen von errechnetem m, um Diskriminante D = 0 zu errechnen:

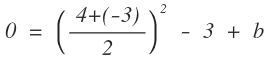
b = + 2,75

Damit erhalten wir als Funktion der Tangente y = -3x + 2,75

Berechnung des Schnittwinkels:

arctan(-1) - arctan(-3) = 26,57°

oder

|arctan(-3)| - |arctan(-1)| = 26,57°

Answer 2

Wie habt ihr denn die Tangentensteigung berechnet. Dazu habt ihr entweder die Ableitung benutzt oder den Differenzialquotienten. Beides ist geeignet um eine Steigung zu ermitteln.

x^2 - 4·x + 3 = -x + 1.75
x = 0.5 und x = 2.5

f(x) = x^2 - 4·x + 3
f'(x) = 2·x - 4

f'(0.5) = -3

arctan(-1) - arctan(-3) = 26.57°