Ich habe folgende Aufgabe in der ei und ej jeweils die Anstrengungen 2er Personen i und j sind. Die Personen stehen in einem Leistungsturnier und können mit der jeweiligen Anstrengung ihren Output qi bzw. qj erhöhen.
Der Output ist je gegeben durch qi = ei + epsilon_i + allgemeiner Störterm.
Es geht darum, dass P(ei,ej) die Wahrscheinlichkeit darstellt, dass das Output qi, welches von ei abhängt, größer ist, als der Output qj von ej.
Soweit alles kein Problem, aber die Übertragung des Ganzen in die Verteilungsfunktion verstehe ich nicht ganz.
Hier das Problem:
Statisches Modell nach Lazear \& Rosen (1981)
Annahmen:
E-Personen-Turnier und beide seien risikoneutral
\( \boldsymbol{m}_{i}=\boldsymbol{e}_{i}+\boldsymbol{\varepsilon}_{i}+\eta \quad(i=1,2) \)
\( q_{i} \) vom \( A G \) beobachtbar und \( e_{i} \) nicht beobachtbar \( \Leftrightarrow \) Rückschlussproblem)
\( \varepsilon_{1} \) und \( \varepsilon_{2} \) identisch und unabhängig voneinander zufallsverteilt
\( g(\cdot): \) Dichtefunktion, \( G(\cdot): \) Verteilungsfunktion
\( c\left(e_{i}\right): \) Arbeitsleid des \( i \) mit \( c^{\prime}(\cdot)>0 \) und \( c^{\prime \prime}(\cdot)>0 \)
\( P: \) Gewinnwahrscheinlichkeit
\( w_{1}: \) Turnierpreis für den Gewinner
\( w_{2}: \) Turnierpreis für den Verlierer \( \Delta w=w_{1}-w_{2}: \) Turnierpreisdifferenz
Kalkül des Agenten \( i \) Maximierung seines Erwartungsnutzens
\begin{aligned}
E U_{i}\left(e_{i}\right) &=P\left(e_{i}, e_{j}\right) \cdot\left[w_{1}-c\left(e_{i}\right)\right]+\left(1-P\left(e_{i}, e_{j}\right)\right)\left[w_{2}-c\left(e_{i}\right)\right] \\
&=P\left(e_{i}, e_{j}\right) \cdot w_{1}+\left(1-P\left(e_{i}, e_{j}\right)\right) w_{2}-c\left(e_{i}\right) \\
&=w_{2}+\Delta w \cdot P\left(e_{i}, e_{j}\right)-c\left(e_{i}\right) \rightarrow \max !
\end{aligned}
Gewinnwarhscheinlichkeit:
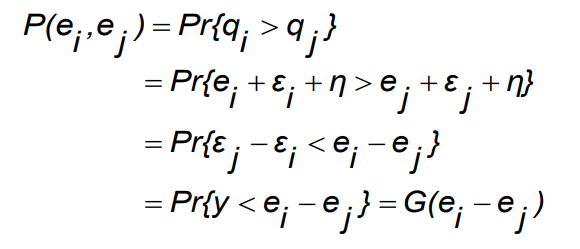
Text erkannt:
\( \begin{aligned} P\left(e_{i}, e_{j}\right) &=\operatorname{Pr}\left\{q_{i}>q_{j}\right\} \\ &=\operatorname{Pr}\left\{\mathrm{e}_{i}+\varepsilon_{i}+\eta>e_{j}+\varepsilon_{j}+\eta\right\} \\ &=\operatorname{Pr}\left\{\varepsilon_{j}-\varepsilon_{i}<\mathrm{e}_{i}-\mathrm{e}_{j}\right\} \\ &=\operatorname{Pr}\left\{y<\mathrm{e}_{i}-\mathrm{e}_{j}\right\}=\mathrm{G}\left(e_{i}-\mathrm{e}_{j}\right) \end{aligned} \)
\( \mathrm{G}(\cdot) \) ist die Verteilungsfunktion der zusammengesetzten
Zufallsvariablen \( y=\varepsilon_{j}-\varepsilon_{i} \)
1. Frage: Was bedeutet die Pr Funktion?
2. Frage: Wie passt die Verteilungsfunktion da rein? Die Umstellung da verstehe ich nicht.
Hier das Ganze noch einmal als Bild zur besseren Lesbarkeit:
