hi! :-)
a)
f(x) = (x+3)e^{-x}
(x+3)e^{-x} = 0
eine nullstelle ablesen(satz vom nullprodukt): x = -3
b)
f(x) = (x+3)*e^{-x} = u*v
f'(x) = u'v + uv' = 1e^{-x} + (x+3)*(-e^{-x})
f'(x) = e^{-x} - e^{-x}(x+3) = e^{-x}(1-x-3) = e^{-x}(-2-x)
= -e^{-x}(2+x)
f''(x) = u'v + uv' = e^{-x}(2+x) -e^{-x}*1
= e^{-x}(2+x) + -e^{-x} = e^{-x}(2+x-1) = e^{-x}(x+1)
c)
gibt es einen hoch- oder tiefpunkt?
f'(x) = -e^{-x}(2+x)
-e^{-x}(2+x) = 0
eine nullstelle ablesen(satz vom nullprodukt): x = -2
an der stelle x = -2 ist die tangente waagerecht, das
ist ein kandidat für einen hoch- oder tiefpunkt.
wir prüfen die zweite ableitung an der stelle x = -2
f''(-2) = e^{-(-2)}((-2)+1) = e^2(-1) = -e^2 < 0
die zweite ableitung an der stelle x = -2 ist kleiner null,
an der stelle x = -2 ist ein hochpunkt.
c)
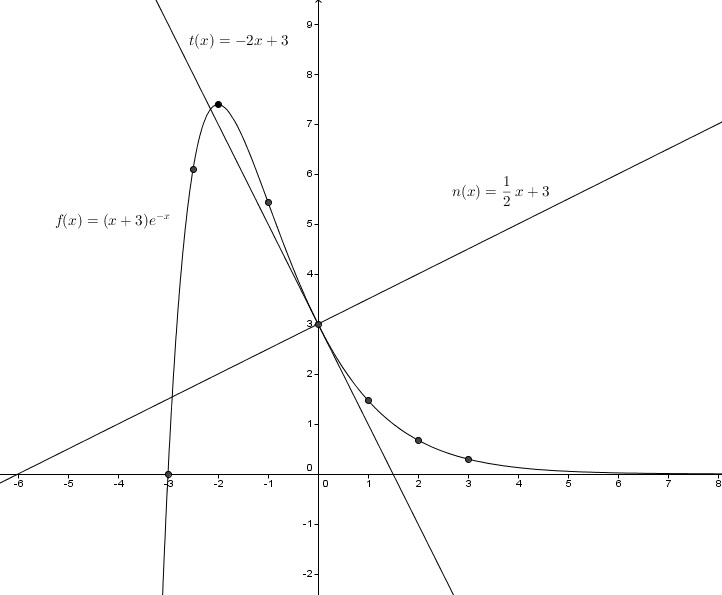
in die werttabelle komme die nullstelle bei x = -3, y = 0
sowie der hochpunkt f(-2) = (-2+3)e^{-(-2)} = e^2 ≈ 7,4
rein, der schnittpunkt des graphen mit der y-achse bei x = 0,
f(0) = (0+3)*e^{-0} = 3 sowie noch ein paar weitere koordinaten.
y 0 6.09 7.4 5.44 3 1.47 0.68 0.3
x -3 -2.5 -2 -1 0 1 2 3
d)
ansatz: punkt-steigungsform
f'(x) = (y-y1)/(x-x1)
f'(x)(x-x1) = (y-y1)
t(x) = f'(x)(x-x1) + y1
x1 = 0, y1 = 3
f'(0) = -e^{-0}(2+0) = -2
t(x) = (-2)(x-0) + 3
t(x) = -2x + 3
n(x) = -1/f'(x) (x-x1) + y1
n(x) = (-1)/(-2) (x-0) + 3
n(x) = 1/2 x + 3