Aufgabe:
Die durchschnittliche Körpermasse von Zwerghamstern wird bei der Geburt mit 1,2 g angegeben, nach 1 Woche mit 4,3 g, nach 2 Wochen mit 8,7 g, nach 3 Wochen mit 12,5 g und nach 4 Wochen mit \( 14,2 \) g.
Die zeitliche Entwicklung der durchschnittlichen Körpermasse von Zwerghamstern soll für die ersten 4 Lebenswochen näherungsweise durch eine Polynomfunktion \( 3 . \) Grades \( f \) beschrieben werden.
1) Ermitteln Sie mithife von Regression eine Gleichung dieser Polynomfunktion 3. Grades \( f . \) Wählen Sie \( t=0 \) für den Zeitpunkt der Geburt.
Zur Zeit \( t_{1} \) gilt: \( f^{\prime \prime}\left(t_{t}\right)=0 \) und \( f^{\prime}\left(t_{1}\right)>0 \)
2) Interpretieren Sie die Bedeutung der Stelle \( t_1 \) im gegebenen Sachzusammenhang.
\( 3,5 \) Wochen nach der Geburt hat ein Zwerghamster \( 62 \% \) der durchschnittlichen Körpermas-
se eines ausgewachsenen Zwerghamsters.
3) Bestimmen Sie mithife der Funktion \( f \), welche durchschnittliche Körpermasse ein ausgewachsener Zwerghamster gemäß diesem Modell hat.
Lösung
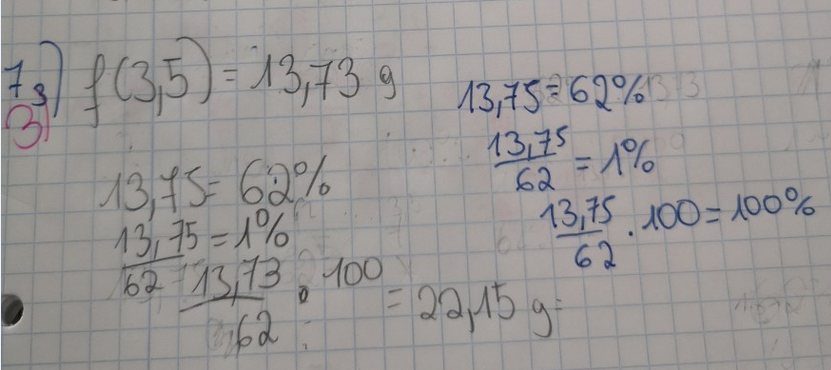
ich brauche bitte nur nummer 3, ich habe es zwar mit dem Lehrer gemacht, jedoch verstehe ich nicht wieso man 13.75 dividiert durch 62 macht, ich dachte 13.75 ist 62