Wer in der Türkei ein Studium beginnen möchte, muss sich einer Hochschulaufnahmeprüfung unterziehen. Wird ein Studium mit Mathematikbezug angestrebt, sind im Rahmen der Prüfung Mathematikaufgaben zu lösen, die sich überwiegend auf den Mittelstufenstoff beziehen und heuristische Fähigkeiten vom Kandidaten erfordern. Eine dieser Fähigkeiten ist das autonome Festlegen von Einheiten. Ein Beispiel:
Im gleichschenklig-rechtwinkligen Dreieck ABC schneidet die Halbierende des Basiswinkels β die Gegenkathete in D.
Bestimme das Längenverhältnis des Streckenzuges BCD und der Hypotenuse AB.
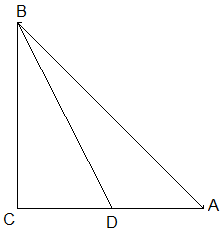
Hier ist es sinnvoll, die Schenkellänge BC als Einheit festzulegen. Wenn dann noch der Satz bekannt ist: ‚Die Winkelhalbierende eines Innenwinkels α im Dreieck teilt die Gegenseite im Verhältnis der anliegenden Seiten‘ ist die Lösung recht schnell gefunden:
BA=√2. D teilt CA im Verhältnis 1:√2. Mit CD=x ergibt sich dann: (1-x)/x=√2und 1/x=√2+1 bzw. x=1/(√2+1)=√2-1. Damit ist das gesuchte Längenverhältnis 1.
Der deutsche Mathematikunterricht der Mittelstufe fordert von den Schülerinnen und Schülern sicher auch heuristische Fähigkeiten, allerdings meistens, ohne diese zuvor zum Unterrichtsgegenstand zu machen. Schon gar nicht wird das autonome Festlegen von Längeneinheiten verlangt. Dazu stand kürzlich ein Beispiel hier im Forum:
Einem Kreis Ka um Mittelpunkt Ma wir ein Kreis Ki um Mittelpunkt Mi so einbeschrieben, dass er Ka von innen und eine Sehne mit der Länge 8 cm in der Mitte berührt, wobei sich über der Sehne ein 120°-Bogen spannt. Wie groß ist das Verhältnis der grünen Fläche von Ki zur gelben Restfläche von Ka ?
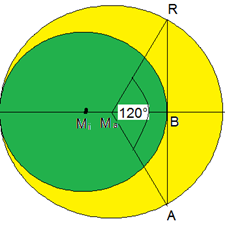
Die Sehne AR wird in dieser Aufgabe auf zwei Arten festgelegt: Durch den Mittelpunktswinkel 120° und durch die Länge 8 cm. Versucht man beide Festlegungen in der Lösung unterzubringen wird die Lösung schwieriger, als wenn man die Angabe ‚8cm‘ außer Acht lässt (auch der Verzicht auf Daten ist eine heuristische Strategie).
Ohne die entbehrliche Längenangabe für die Sehne wäre dies sicher eine Aufgabe für die türkische Hochschulaufnahmeprüfung und ein hypothetischer Kandidat hätte sie so gelöst:
Der Radius des großen Kreises wird als Längeneinheit gewählt. Dann ist der große Kreis ein Einheitskreis mit der Fläche π. MBR ist ein halbes gleichseitiges Dreieck. Dann ist MB=1/2 und der kleine Kreis hat den Radus ¾ sowie die Fläche (3/4)2⋅π. (3/4)2⋅π/π=9/16. Das Flächenverhältnis der Kreise ist 9:16 und das gesuchte Flächenverhältnis ist 9:7.