Hallo Torsten,
Muss ich jetzt für alle drei strecken das jeweils 3 mal überprüfen, also insgesamt 9 Rechnungen anfertigen?
Im Prinzip schon, aber man kann sich das Leben etwas erleichtern, indem man genauer hinschaut.
Bei den Punkten \(A\) und \(B\) ist die x-Koordinate =0.D.h. bei jedem Punkt, der auf einer Geraden durch \(A\) und \(B\) liegt, muss die x-koordinate genauso =0 sein. Das ist aber bei keinem der drei Punkte \(P\), \(Q\) und \(R\) der Fall.
Ich komme gerade nicht weiter nach der ersten Strecke also AB, da hab ich nämlich raus, dass keiner der Punkte auf der strecke liegt
folglich ist das richtig!
Nehmen wir uns dann die Strecke \(BC\) vor. Bei den drei Punkten \(P\), \(Q\) und \(R\) ist die x-Koordinate =2. D.h. wir müssen auf der Strecke \(BC\) nur den Punkt berechnen, wo \(x=2\) ist - also$$g_{BC}: \space x = B + t(C-B) = \begin{pmatrix} 0\\ 6\\ 3\end{pmatrix} + t \begin{pmatrix} 3\\ -3\\ -3\end{pmatrix}$$für \(t=2/3\) wird die x-Koordinate der Geraden =2$$x \left(t=\frac 23 \right) = \begin{pmatrix} 0\\ 6\\ 3\end{pmatrix} + \frac 23 \begin{pmatrix} 3\\ -3\\ -3\end{pmatrix} = \begin{pmatrix} 2\\ 4\\ 1\end{pmatrix} = Q$$und dies ist die Position von \(Q\). Und dies ist der einzige Punkt der auf \(BC\) liegt. Der Vollständigkeit halber sei noch erwähnt, dass das \(t\) im Intervall \([0;\, 1]\) liegen muss. Ansonsten läge der Punkt zwar auf der Geraden, aber außerhalb der Strecke.
Bei \(g_{ca}\) geht man genauso vor. Das überlasse ich jetzt Dir. Bestimme den Punkt von \(g_{ca}\), wo die x-Koordinate =2 wird und vergleiche das Ergebnis mit den drei Punkten.
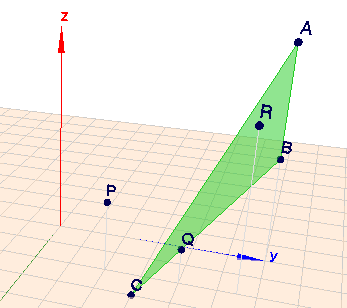
Man kann natürlich auch alle Punkte in Geoknecht3D eingeben, dann 'sieht' man das Ergebnis. Klick auf das Bild, dann öffnet sich die Szene in Geoknecht3D.
Gruß Werner