Varianz berechnen mit vorgegebenen Werten

Question

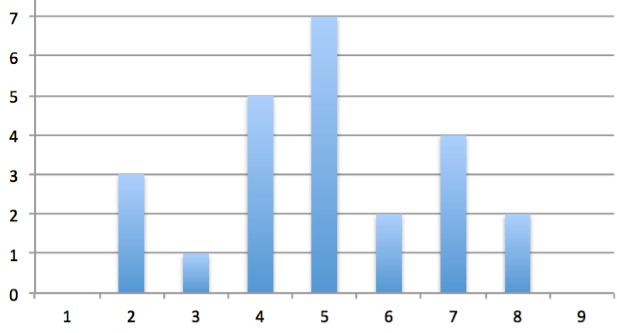
Ich arbeite eine weitere Vorlesung durch. Dort ist die obige Darstellung abgebildet.

Ich soll nun die Varianz und das arithmetische Mittel angeben. 

Beide Werte sind in den folgenden Folien auch benannt.

Arithmetische Mittel = 5

Varianz = 3

Das arithemtische Mittel kann ich rechnerisch nachvollziehen. Bei der Berechnung der Varianz gelingt es mir einfach nicht. Ich komme jedes mal auf andere Werte.

Die Formel zur Berechnung lautet in meinen Folien 

\( \mathrm{s}^{2}=\frac{1}{\mathrm{n}} \sum \limits_{\mathrm{i}=1}^{\mathrm{n}}\left(\mathrm{x}_{\mathrm{i}}-\overline{\mathrm{x}}\right)^{2} \)

Mein Berechnungsversuch:

s² = 1/9 [ (0-5)² + (3-5)² + (1-5)² + (5+5)² + (7-5)² + (2+5)² + (4-5)² + (2-5)² + (0+5)² ]

           = 1/9 * [93]

           = 10,33

Ich finde meinen Fehler nicht. Sieht vielleicht jemand meinen Fehler?

Answer 1

Aloha :)

Die Formel ist falsch, das ist aber vermutlich nur eins von deinen 2 Problemen.

Die Varianz ist definiert als:$$V(X)=\frac{1}{N}\sum\limits_{i=1}^N\left(x_i-\mu_x\right)^2$$Darin ist \(\mu_x\) der exakte Erwartungswert der Zufallsvariablen \(X\). Der ist aber oft nicht bekannt, etwa wenn man nur eine Stichprobe betrachtet. In diesen Fällen kann der Erwartungswert durch den Mittelwert genähert werden: \(\mu_x\approx\overline x\). Der Mittelwert \(\overline x\) enthält aber eine Abweichung bzw. Ungenauigkeit gegenüber dem exakten Erwartungswert \(\mu_x\). Diese Ungenauigkeit pflanzt sich in die Varianzformel fort und führt zu einer Erhöhung der Varianz. Die korrekte Formel ist daher:$$V(X)=\frac{1}{N-1}\sum\limits_{i=1}^N\left(x_i-\overline x\right)^2$$Beachte, dass darin der Erwartungswert \(\mu_x\) durch den Mittelwert \(\overline x\) als Näherung ersetzt wurde. Dafür wird als Korrektur nicht durch \(N\), sondern durch \(N-1\) dividiert.

Weiter musst du bei der Berechnung von Mittelwert und Varianz beachten, dass z.B. der Wert 5 genau 7-mal vorkommt oder der Wert 6 genau 2-mal...

Comments

Danke für deine Hinweise. Auf deine untere Formel bin ich bei meinen Recherchen auch gestoßen; denke aber, da in den Vorlesungsfolien eine abweichende Formel vermerkt ist, sollte man irgendwie auch mit dieser vorgegebenen Formel auf das Ergebnis Varianz=3 kommen. Ich werde es weiter probieren und dabei mal deine Formeln um Hinterkopf behalten.

---

Was in der Vorlesung gesagt wird, muss nicht richtig sein. Die Formel von deinem Prof ist Unsinn. Er/ Sie vermischt Gesamtheit und Stichprobe.

---

Ist mir schon öfter aufgefallen. Da scheint es keine Qualitätsansprüche zu geben, geschweige denn Qualitätskontrolle stattzufinden. Mich treibt sowas zur Verzweiflung. Sowas kostet einen Studenten extrem viel Arbeitszeit. Und dann wundern die sich, wenn vermehrt die Studenten der Vorlesung fern bleiben...naja, egal...anderes Thema :-)

Ich versuche dran zu bleiben.

---

Ich konnte mein Problem lösen. Es werden aber tatsächlich unterschiedliche Formelangaben gemacht; ich bin bei meinen weiteren Recherchen (zumindest Online) auf beide Formeln gestoßen und beide scheinen ihre Berechtigung zu haben und richtig zu sein. Interessant wäre es jetzt in Erfahrung zu bringen, warum sich nicht "die eine" Formel durchgesetzt hat und in der Literatur tatsächlich unterschiedliche Formelangaben gemacht werden. Aber das ist eher eine Aufgabe fürs nächste Semester. Danke nochmals.

---

Ich sehe da eher ein Problem das bei der Tabelle nicht angegeben ist ob es sich dabei um eine Stichprobe oder eine Vollerhebung handelt. Wenn es eine Vollerhebung ist dann kann man bei der Varianz durch n statt n + 1 teilen.

Answer 2

Woher kommt dein (1/9)?

Du hast 24 Werte. (Dreimal die 2, einmal die 3, fünfmal die 4,...)

Comments

Ok. Ich gehe davon aus, dass die Ergebnisse dann mit einer Tabellenkalkulation berechnet wurden. Die Rechnung würde ja sonst extrem lang und unübersichtlich werden. Danke für den Hinweis. Ich werde mal versuchen, dass ganze in Excel durchzuspielen.

---

Ich bin zu dem Zeitpunkt von 9 Werten ausgegangen. Dein Hinweis mit den "doppelten Werten" hat mir auf jeden Fall beim lösen ähnlicher Aufgaben geholfen. Danke für die Hilfestellung.

Answer 3

Arithmetisches Mittel

μ = (2·3 + 3·1 + 4·5 + 5·7 + 6·2 + 7·4 + 8·2)/24 = 5

Varianz

σ^2 = (2^2·3 + 3^2·1 + 4^2·5 + 5^2·7 + 6^2·2 + 7^2·4 + 8^2·2)/24 - 5^2 = 3