Zu a)
Betrachte folgende Skizze:
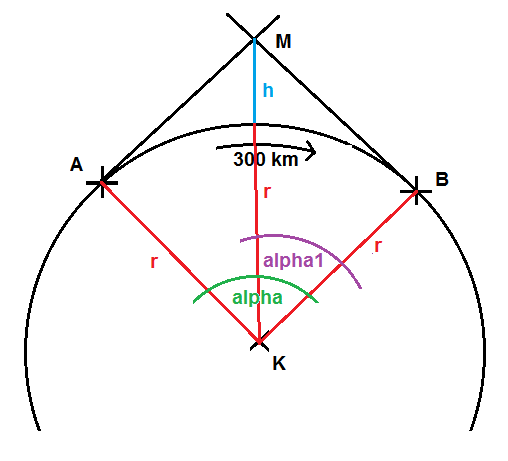
Da eine Kreistangente immer senkrecht auf dem Kreisradius steht, ist das Dreieck MBK rechtwinklig mit der Hypotenuse ( r + h ) und dem rechten Winkel bei B. Also gilt:
MB 2 + r 2 = ( r + h ) 2
Der Mittelpunktswinkel alpha verhält sich zu 360° wie die Strecke 300 km zum Gesamtumfang des Kreises, also:
alpha / 360 = 300 / ( 2 * pi * 6370 )
<=> alpha = 360 * 300 / ( 2 * pi * 6370 ) = 2,7° (gerundet)
Da der Ballon mittig zwischen A und B aufsteigen soll, ist die Gerade KM Winkelhalbierende des WInkels alpha und somit gilt:
alpha1 = alpha / 2 = 1,35°
Daraus ergibt sich für die Strecke MB:
tan ( alpha1 ) = MB / r
<=> MB = r * tan ( alpha1 )
Das Gleichungssystem aus den beiden Fett gesetzten Gleichungen ist nun zu lösen:
Aus der ersten Gleichung
MB 2 + r 2 = ( r + h ) 2
ergibt sich:
<=> r + h = √ ( MB 2 + r 2 )
<=> h = √ ( MB 2 + r 2 ) - r
Mit MB 2 = r 2 * tan 2 ( alpha1 ) (das folgt aus der zweiten Gleichung) erhält man durch Einsetzen:
h = √ ( r 2 * tan 2 ( alpha1 ) + r 2 ) - r
= √ ( r 2 * ( 1 + tan 2 ( alpha1 ) ) ) - r
= r * √ ( 1 + tan 2 ( alpha1 ) ) - r
= r * ( √ ( 1 + tan 2 ( alpha1 ) ) - 1 )
Bekannte Werte einsetzen:
h = 6370 * ( √ ( 1 + tan 2 ( 1,35° ) ) - 1 ) = 1,77 km
Der Ballon muss also etwa 1,77 km hoch aufsteigen, um beide Stationen "sehen" zu können.
In der zweiten Situation soll der Ballon senkrecht über A aufsteigen. Das sieht dann so aus:
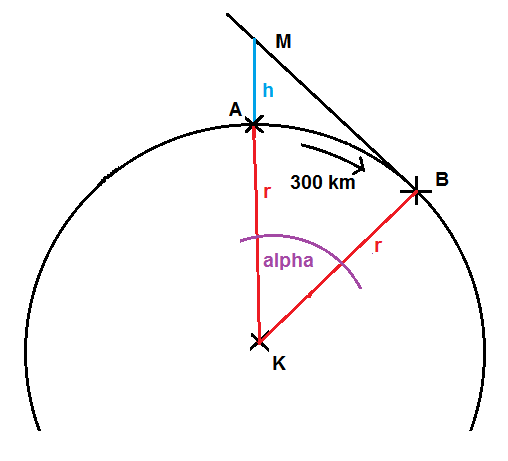
Wieder ist MBK ein rechtwinkliges Dreieck. Wieder kann man den Winkel alpha bestimmen, indem man rechnet::
alpha = 360 * 300 / ( 2 * r * pi )
Ähnlich wie oben kann man nun mit Hilfe des Satzes des Pythagoras und mit dem Tangens des Mittelpunktswinkels die Strecke MB und die Höhe h bestimmen. Das aber möchte ich nun dir überlassen.
Zur Kontrolle:
h = 7,08 km