Aufgabe:
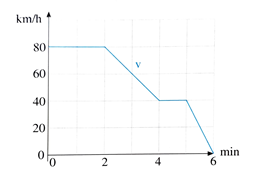
Der Fahrtenschreiber hat die Geschwindigkeit eines Busses zwischen zwei Haltestationen aufgezeichnet.
(a) Stellen Sie die Geschwindigkeitsfunktion v als abschnittsweise definierte Funktion dar.
(b) Wie weit liegen die Haltestellen voneinander entfernt?
Problem/Ansatz:
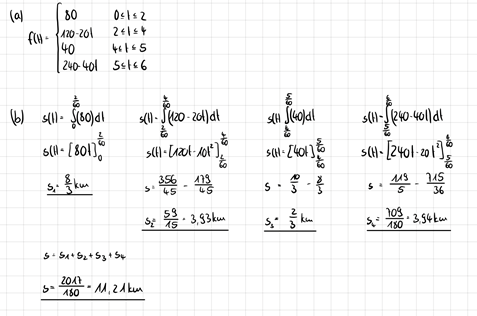
Text erkannt:
(a) \( f(H)=\left\{\begin{array}{ll}80 & 0 \leq t \leq 2 \\ 120-201 & 2 \leqslant 1 \leqslant 4 \\ 40 & 46 t \leq 5 \\ 240-401 & 5 \leq t \leq 6\end{array}\right. \)
(b) \( s(\|)=\int \limits_{0}^{\frac{2}{5}}(80) d t \quad s\left(H-\int \limits_{\frac{2}{60}}^{\frac{4}{50}}\left((120-20 t) d t \quad s\left(H \int \limits_{\frac{2}{6}}^{\frac{5}{60}}(40) d l \quad s(t)-\int \limits_{\frac{5}{5}}^{5}(240-40 t) d t\right.\right.\right. \)
\( s\left(H=[80 t]_{0}^{\frac{2}{60}} \quad s(t)=\left[120 t-10 t^{2}\right]_{\frac{2}{60}}^{\frac{4}{60}} \quad s(H)=[40 t]_{\frac{4}{60}}^{\frac{5}{60}} \quad s(t)=\left[2401-20 t^{2}\right]_{\frac{5}{60}}^{\frac{4}{60}}\right. \)
\( s+\frac{8}{3} k m=\frac{356}{45}=\frac{173}{45} \quad s=\frac{10}{3}-\frac{8}{3} \quad s=\frac{\mu 1}{5}-\frac{715}{36} \)
\( \underline{s_{2}}=\frac{59}{15} \cdot 3,93 \mathrm{~km} \quad s_{3}=\frac{2}{3} \mathrm{~km} \quad s_{4}=\frac{709}{180} \cdot 3,54 \mathrm{~km} \)
\( S+S_{1}+S_{2}+S_{3}+S_{4} \)
\( b=\frac{2017}{180}=A_{1} 2 A \mathrm{ken} \)
Wie meinem Ansatz zu entnehmen ich habe ich Aufgabe (a) bereits lösen können. Allerdings habe ich das Problem, dass ich bei (b) nicht auf das richtige Ergebnis nämlich 5,67km komme.
Ich hoffe ihr könnt mir weiterhelfen und vielen Dank schonmal im Voraus.