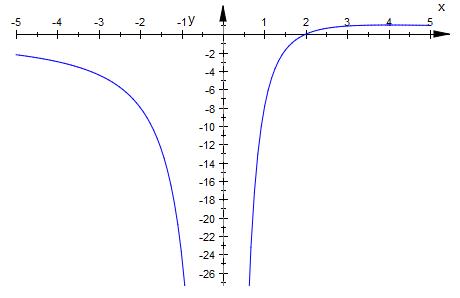
f = (8x-16) / x^2
Polstelle bei x = 0
f = (8*0-16) / 0^2 = -16 / 0 = -∞
x = 0 ist eine vertikale Asymptote ( y-Achse )
Verhalten im Unendlichen
lim x -> + ∞ [ (8x-16) / x^2 ] = 8 / x - 16 / x^2 = 8 / x = 0
lim x -> - ∞ [ (8x-16) / x^2 ] = -8 / x - 16 / x^2 = -8 / x = 0
y = 0 ist eine horizontale Asymptote ( x-Achse )