Hallo Lauradoto,
ich unterstelle mal, dass Dir bei den Koordinaten von \(P\) ein Fehler unterlaufen ist. Die Koordinaten könnten lauten:$$P= \begin{pmatrix} \colorbox{#ffff00}{+}2\\ -1\\ 0\end{pmatrix}, \quad Q= \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix}, \quad R= \begin{pmatrix}2\\ 3\\ -4\end{pmatrix}$$Dann sind die Seiten \(PQ\) und \(QR\) gleich lang. Das Dreieck ist somit gleichschenklig und die Symmetrieachse geht durch \(Q\) und den Mittelpunkt \(M_q\) von \(PR\)$$\begin{aligned} M_q &= \frac 12(P + R) \\&=\frac 12 \left( \begin{pmatrix}2\\ -1\\ 0\end{pmatrix} + \begin{pmatrix}2\\ 3\\ -4\end{pmatrix}\right) \\&= \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} \end{aligned}$$Die Gerade \(g\) durch \(M_q\) und \(Q\) ist dann$$\begin{aligned} g: \space x &= Q + t(M_q-Q) \\&= \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + t \left( \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} - \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix}\right) \\&= \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + t \begin{pmatrix}4\\ 0\\ 0\end{pmatrix}\end{aligned}$$Wenn nun ein Wert für \(t\) existiert, so dass \(x(t) = S\) ist, dann liegt \(S\) auf \(g\).$$S = \begin{pmatrix}1\\ 1\\ -2\end{pmatrix} = \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + t \begin{pmatrix}4\\ 0\\ 0\end{pmatrix}$$In der ersten Zeile steht \(1 = -2 + 4t\). Daraus folgt \(t = 3/4\). Einsetzen in die Geradengleichung gibt:$$x\left( t= \frac 34\right) = \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + \frac 34 \begin{pmatrix}4\\ 0\\ 0\end{pmatrix} = \begin{pmatrix}1\\ 1\\ -2\end{pmatrix} = S$$also liegt der Punkt \(S\) auf der Geraden.
Und so sieht das aus:
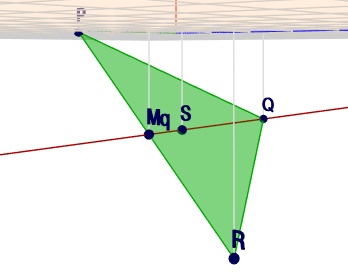
(klick auf das Bild)