Geometrie vektoren rechnen

Question

Aufgabe:

… p(-2/-1/0), Q(-2/1/-2), R(2/3/-4) S(1/1/-2)

Bestimme eine geradengleichung der Symmetrieachse des Dreiecks.

Zeige dass S auf die Symmetrieachse liegt.

Comments

Hallo,

das Dreieck $\triangle PQR$ hat keine Symmetrieachse. Der Punkt $S$ liegt aber auf der Verlängerung der Seitenhalbierenden (bzw. der Schwerelinie) durch $Q$.

---

Geometrie Vektoren rechnen, die anderen Vektoren schlafen

Answer 1

Bestimme eine Geradengleichung der Symmetrieachse des Dreiecks PQR.

Das Dreieck PQR ist nicht gleichschenklig und hat folglich keine Symmetrieachse.

Answer 2

Hallo Lauradoto,

ich unterstelle mal, dass Dir bei den Koordinaten von $P$ ein Fehler unterlaufen ist. Die Koordinaten könnten lauten:$$P= \begin{pmatrix} \colorbox{#ffff00}{+}2\\ -1\\ 0\end{pmatrix}, \quad Q= \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix}, \quad R= \begin{pmatrix}2\\ 3\\ -4\end{pmatrix}$$Dann sind die Seiten $PQ$ und $QR$ gleich lang. Das Dreieck ist somit gleichschenklig und die Symmetrieachse geht durch $Q$ und den Mittelpunkt $M_q$ von $PR$$$\begin{aligned} M_q &= \frac 12(P + R) \\&=\frac 12 \left( \begin{pmatrix}2\\ -1\\ 0\end{pmatrix} + \begin{pmatrix}2\\ 3\\ -4\end{pmatrix}\right) \\&= \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} \end{aligned}$$Die Gerade $g$ durch $M_q$ und $Q$ ist dann$$\begin{aligned} g: \space x &= Q + t(M_q-Q) \\&= \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + t \left( \begin{pmatrix}2\\ 1\\ -2\end{pmatrix} - \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix}\right) \\&= \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + t \begin{pmatrix}4\\ 0\\ 0\end{pmatrix}\end{aligned}$$Wenn nun ein Wert für $t$ existiert, so dass $x(t) = S$ ist, dann liegt $S$ auf $g$.$$S = \begin{pmatrix}1\\ 1\\ -2\end{pmatrix} = \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + t \begin{pmatrix}4\\ 0\\ 0\end{pmatrix}$$In der ersten Zeile steht $1 = -2 + 4t$. Daraus folgt $t = 3/4$. Einsetzen in die Geradengleichung gibt:$$x\left( t= \frac 34\right) = \begin{pmatrix}-2\\ 1\\ -2\end{pmatrix} + \frac 34 \begin{pmatrix}4\\ 0\\ 0\end{pmatrix} = \begin{pmatrix}1\\ 1\\ -2\end{pmatrix} = S$$also liegt der Punkt $S$ auf der Geraden.

Und so sieht das aus:

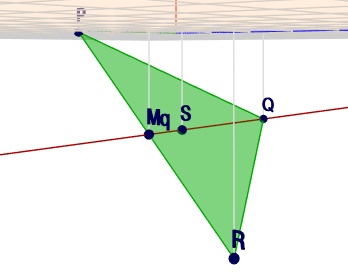
(klick auf das Bild)