Aloha :)
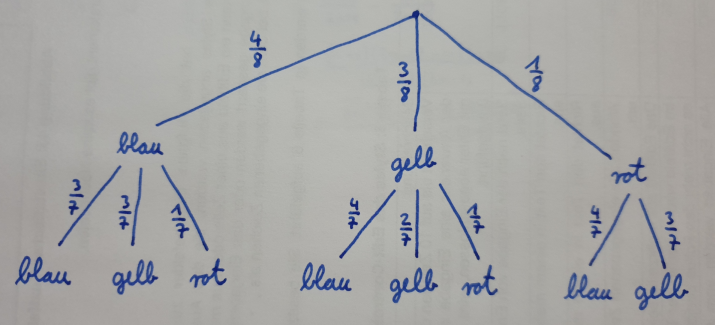
Kugeln: 4 blaue + 3 gelbe + 1 rote
Folgende Paar-Konstellationen sind möglich.$$(bb),(bg),(br),(gg),(gb),(gr),(rb),(rg)$$Die Wahrscheinlichkeit für jedes dieser Ereignisse ist:
$$P(bb)=\frac{4}{8}\cdot\frac{3}{7}=\frac{12}{56}$$$$P(bg)=\frac{4}{8}\cdot\frac{3}{7}=\frac{12}{56}$$$$P(br)=\frac{4}{8}\cdot\frac{1}{7}=\frac{4}{56}$$$$P(gg)=\frac{3}{8}\cdot\frac{2}{7}=\frac{6}{56}$$$$P(gb)=\frac{3}{8}\cdot\frac{4}{7}=\frac{12}{56}$$$$P(gr)=\frac{3}{8}\cdot\frac{1}{7}=\frac{3}{56}$$$$P(rb)=\frac{1}{8}\cdot\frac{4}{7}=\frac{4}{56}$$$$P(rg)=\frac{1}{8}\cdot\frac{3}{7}=\frac{3}{56}$$
Ich kann am Rechner leider nicht so gut zeichnen, weil ich mich mit diesen Zeichentools nicht beschäftigt habe.