Zylinderförmiges Dessert in einer Dessertschale

Question

Aufgabe: Konnte a bis c bestens lösen. Bei d) weiss ich folgendes;

Untere Grenze ist unbekannt für den Rand, also habe ich die untere Grenze = z gesetzt (kann auch eine andere Variable sein). Die Höhe ist somit auch bekannt, undzwar h=10-z (Ablesbar von Darstellung. Wie komme ich nun auf r und wie kann man das am ende, wenn ich r und h in die Volumenformel des Zylinders einsetze maximieren?

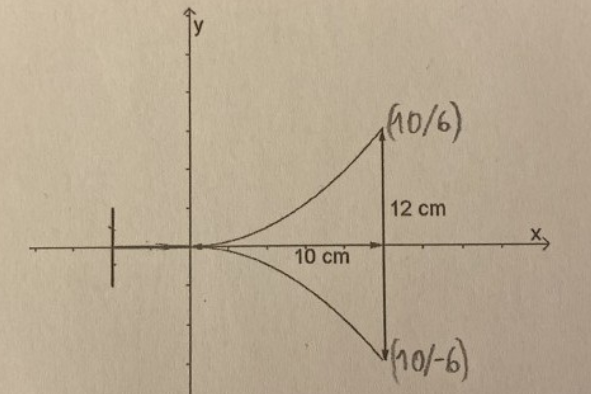
Eine Dessertschale besitzt eine Öffnung von \( 12 \mathrm{cm} \) und eine Tiefe von \( 10 \mathrm{cm} \) Denkt man sich die Dessertschale liegend, so wird der Rand ihrer Querschnittsfläche im ersten und vierten Quadranten durch Parabeln \( 2 . \) Ordnung begrenzt (vgl. Zeichnung).

a. Bestimmen Sie die Funktionsgleichung für die Parabel im ersten Quadranten.
Rechnen Sie mit der falschen Funktion \( f(x)=0.08 x^{2} \) weiter, falls Sie Teilaufgabe a. nicht gelöst haben.

b. Berechnen Sie das Fassungsvermögen der Dessertschale.

c. In die Dessertschale wird 1.5 dI Crème gegossen. Bis zu welcher Höhe ist die Schale gefüllt?
d. Statt Crème wird in der Schale ein möglichst grosses zylinderformiges festes Dessert serviert, das nicht über den Rand hinausschauen soll. Berechnen Sie seine Höhe.

Problem/Ansatz:

Answer 1

d)
V = pi·f(a)^2·(10 - a) = pi·(0.06·a^2)^2·(10 - a) = 9/250·pi·a^4 - 9/2500·pi·a^5
V' = 18/125·pi·a^3 - 9/500·pi·a^4 = 0 → a = 8

Damit ist die Höhe 10 - 8 = 2 cm.

Comments

deine Lösung kann ich echt gut nachvollziehen.

Answer 2

 Der Punkt (10-h|r) muss die Parabelgleichung erfüllen.

Dann hast du eine Nebenbedingung, welche in die Hauptbedingung eingesetzt wird.

Comments

Also meinst du in y=3/50x^2 für y r einsetzen und für x (10-h) einsetzen?

Bekomme dann r= 3/50•(3h^2-60h+300)

Ist es das was du meinst?

---

Also meinst du in y=3/50x2 für y r einsetzen und für x (10-h) einsetzen?

Ja, das meine ich.
Bekomme dann r= 3/50•(3h²-60h+300)

Ich bekomme dann r= 3/50•(h²-20h+100)