.. ich bin anscheinend etwas zu spät dazu gekommen ;-)
Wenn man in der Zeichnung das überflüssige weg lässt (Z.B die Punkte \(J\) und \(K\) und ihre angrenzenden Seiten) und von den Dreiecken jeweils die Höhen einzeichnet, mit denen sie auf dem Quadrat \(BDGC\) stehen, so tuen sich sehr viele Paare identischer rechtwinkliger Dreiecke auf:
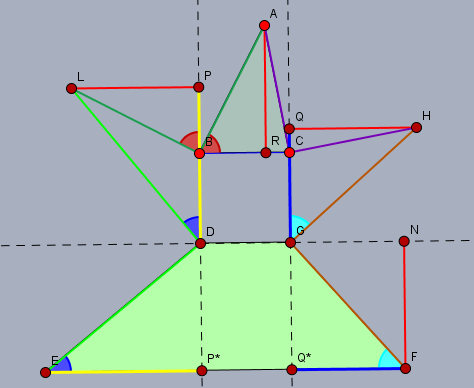
In obigem Bild sollen gleiche Strecken und Winkel mit gleicher Farbe gleich groß sein. Da z.B. das Dreieck \(\triangle BPL\) identisch zu \(\triangle BRA\) ist (u.a. entsprechend), sind alle Höhen \(RA\), \(PL\), \(QH\) und \(NF\) (rot) identisch. Da weiter die Dreiecke \(\triangle DPL\) und \(\triangle EP^*D\) sowie die beiden Dreiecke \(\triangle GHQ\) und \(GQ^*F\) gleich sind, sind natürlich auch die Strecken \(|DP|=|EP^*|\) sowie \(|GQ|=|FQ^*|\).
Und da \(|BP|=|BR|\) und \(|CQ|=|CR|\) ist \(|DP|+|GQ|=3|BC|\). Also ist \(|EF| = 3|BC| + |P^*Q^*| = 4|BC|\). Und dass daraus $$F_{EFGD} = 5 \cdot F_{ABC}$$folgt, ist dann nur noch Formsache.
Gruß Werner