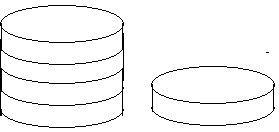
Die meisten Spielsteine für Brettspiele sind zylindrisch und lassen sich stapeln. Aus 5 Spielsteinen werden (zufällig) diese Stapel gebildet:
Dann wird folgendes Solitärspiel gestartet:
1. Spielzug: Der Spielstein ganz rechts wird aufgenommen und auf den Turm links davon gelegt:
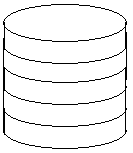
2. Spielzug: Der Turm wird aufgenommen und Stein für Stein ausgelegt:

Spielzug allgemein: Der Turm ganz rechts wird aufgenommen und auf die Türme links davon einzeln und der Reihe nach verteilt. Wenn kein Turm mehr vorhanden ist, werden „Türme“ aus je einem Stein gebildet.
Wenn wir, statt Türme zu zeichnen, Turmhöhen aufschreiben, sieht das so aus:
[4, 1]
[5]
[1, 1, 1, 1, 1]
[1, 1, 1, 2]
[1, 2, 2]
[2, 3]
[1, 1, 3]
[1, 2, 2]
An dieser Stelle können wir das Spiel abbrechen, denn die Folge der Turmhöhen 1, 2, 2, hat sich wiederholt und so wird sich der darauf folgende Zyklus nun ständig wiederholen.
Die nachfolgende Grafik zeigt, dass alle Startkonstellationen von Türmen aus 5 Spielsteinen in die Folge von Turmhöhen 1, 2, 2 einmünden:
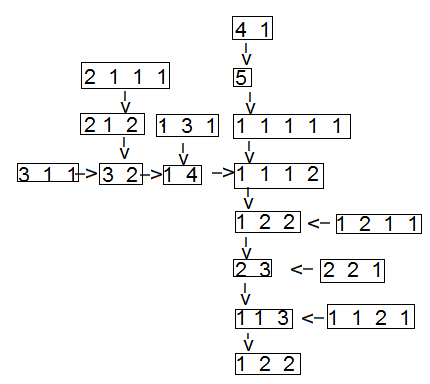
Es lässt sich vermuten, dass dies Spiel für jede Anzahl von Spielsteinen in jeder frei gewählten Startkonstellation in einem Zyklus endet. Damit haben wir eine erste Hypothese zu diesem Spiel.
Eine große Zahl weiterer Hypothesen drängt sich auf, wenn man dieses Spiel wiederholt spielt. Dabei ist es möglicherweise zweckmäßig, den Spielverlauf mittels Computer zu simulieren.
Das Spiel selbst wird beschrieben bei Klaus Hasemann, Ulrich Leonhardt, Horst Szambien, „Denkaufgaben für die 1.und 2. Klasse“, Cornelsen Verlag GmbH & Co., Berlin, Reihe ‚Eins plus, Begabungen fördern im Mathematikunterricht‘, 2006, ISBN 978-3-589-22146-2. Der Titel lässt nicht erkennen, dass im Rahmen dieses Spieles Hypothesen aufgestellt werden können, deren Beweis erst in höheren Klassenstufen geführt werden können und sogar im Studium gute Kenntnisse der Zahlentheorie erfordern.
Wer dazu Näheres wissen will, folge dem Link https://link.springer.com/article/10.1007/s00591-012-0107-4