Produkt möglichst billig herstellen + optimale Werte bestimmen

Question

Aufgabe: Ein Unternehmen möchte 50 Einheiten eines Produkts so billig wie möglich herstellen . Unter Verwendung von K Einheiten Kapital und L Einheiten Arbeit können√K +L Einheiten hergestellt werden. Die Kosten für Kapital und Arbeit seien 1 bzw. 20. Bestimmen Sie die optimalen Werte für K und L.

Problem/Ansatz:

Ich weiß nicht wie ich es rechnen soll. Wir sind geraden beim Thema Linearisierungen und Extrema aber ich glaube nicht das es was mit der Linearisierungen und Extrema zu tun hat und das verwirt mich irgendwie noch mehr. Deswegen ist der Fragetitel auch komisch aber ich weiß einfach nicht wo das hingehört.

Answer 1

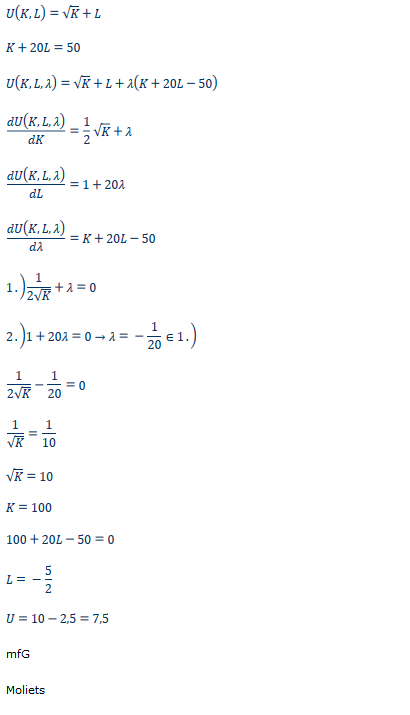
Text erkannt:

\( U(K, L)=\sqrt{K}+L \)
\( K+20 L=50 \)
\( U(K, L, \lambda)=\sqrt{K}+L+\lambda(K+20 L-50) \)
\( \frac{d U(K, L, \lambda)}{d K}=\frac{1}{2} \sqrt{K}+\lambda \)
\( \frac{d U(K, L, \lambda)}{d L}=1+20 \lambda \)
\( \frac{d U(K, L, \lambda)}{d \lambda}=K+20 L-50 \)
1. \( ) \frac{1}{2 \sqrt{K}}+\lambda=0 \)
2. \( ) 1+20 \lambda=0 \rightarrow \lambda=-\frac{1}{20} \in 1 . \)
\( \frac{1}{2 \sqrt{K}}-\frac{1}{20}=0 \)
\( \frac{1}{\sqrt{K}}=\frac{1}{10} \)
\( \sqrt{K}=10 \)
\( K=100 \)
\( 100+20 L-50=0 \)
\( L=-\frac{5}{2} \)
\( U=10-2,5=7,5 \)
\( \mathrm{mfG} \)
Moliets