Ich habe mal nicht den Definitionsbereich eingeschränkt, Aber das könnte so aussehen:
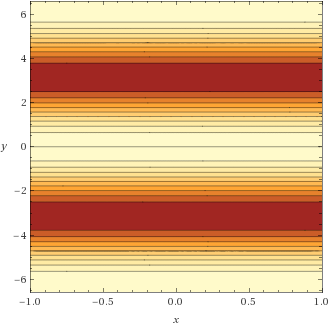
In einer 3D-Darstellung dann wie folgt
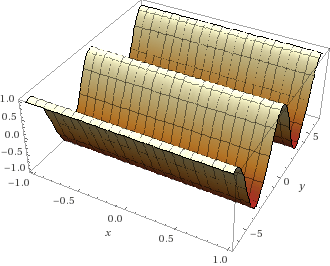
Hier nochmals mit Einschränkung des Definitionsbereiches
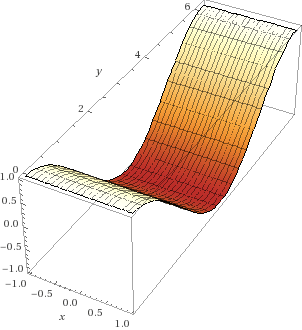
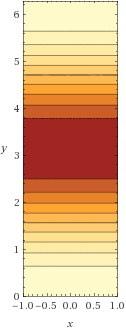
Unterteile eventuell den Wertebereich von -1 bis 1 in 10 Schritte a 0.2. Und dann berechnest du jeweils an welcher stelle y diese Höhe erreicht wid.
[-1, 3.141592653;
-0.8, 2.498091544;
-0.6, 2.214297435;
-0.4, 1.982313172;
-0.2, 1.772154247;
0, 1.570796326;
0.2, 1.369438406;
0.4, 1.159279480;
0.6, 0.9272952180;
0.8, 0.6435011087;
1, 0]
Dann haben wir die gleichen Werte nochmals Spiegelverkehrt im Bereich von pi bis 2pi.
Ist das soweit klar?