Man bestimme mittels des äußeren Produkts (Kreuzprodukts) den Flächeninhalt des Parallelogramms

Question

Es seien a und b Einheitsvektoren des V³O, die einen Winkel von 45° miteinander einschließen.

Man bestimme mittels des äußeren Produkts (Kreuzprodukts) den Flächeninhaltdes Parallelogramms, dessen Seiten durch die Vektoren u := 2a-b und v := 4a-5b gegeben sind.

und nochmal kurz erklären , was genau ein Kreuzprodukt ist bitte! 

:-)

Answer 1

A soll ein beliebiger Einheitsvektor sein, also z.B.

a = ( 1 | 0 | 0 )

b = ( b₁ | b₂ | b₃ ) soll ebenfalls ein Einheitsvektor sein. Der Einfachheit halber setzt man die Koordinate b₃ = 0 . Dies tut den geforderten Eigenschaften von b (Einheitsvektor, 45 ° zu a) keinen Abbruch, vereinfacht aber die Berechnungen. 

Für b muss also gelten:

| b | = √ ( b₁² + b₂² + 0 ² ) = 1

<=> b₁² + b₂² = 1 (Gleichung 1)

Außerdem soll b mit a einen Winkel von 45 ° einschließen, es muss also gelten:

b₁ / b₂ = tan ( 45 °) = 1

<=> b₁ = b₂

Einsetzen in Gleichung 1 ergibt:

2 * b₁² = 1

<=> b₁ = 1 / √ 2

und wegen b₁ = b₂

=> b₂ = 1 / √ 2

Somit gilt also:

b = ( 1 / √ 2  | 1 / √ 2 | 0 )

Dieser Vektor hat die Länge 1, ist also Einheitsvektor, und schließt mit a einen Winkel von 45 ° ein.

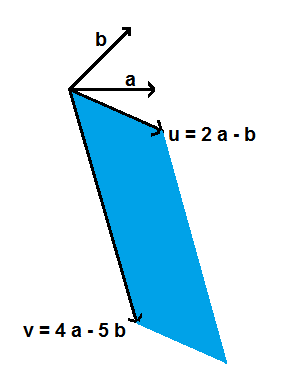
Nun kann man die Vektoren u und v berechnen:

u = 2 a - b = ( 2 - 1 / √ 2 | - 1 / √ 2 | 0 )

v = 4 a - 5 b = ( 4 - 5 / √ 2 | - 5 / √ 2 | 0 )

und daraus das Kreuzprodukt berechnen.

Einschub:

Das Kreuzprodukt zweier Vektoren r und s  ist ein Vektor, der senkrecht auf der durch r und s aufgespannten Ebene steht. Der Wert seines Betrages (also seine Länge) ist gleich dem Wert des Flächeninhaltes des von r und s begrenzten Parallelogramms. 

Das Kreuzprodukt zweier Vektoren r = ( r₁ | r₂ | r₃ ) und  s = ( s₁ | s₂ | s₃ ) berechnet man folgendermaßen:

r x s = ( r₂ * s₃ - r₃ * s₂ | r₃ * s₁ - r₁ * s₃ | r₁ * s₂ - r₂ * s₁ )

Ende Einschub

Das Kreuzprodukt u x v ist also demgemäß:

u x v = ( u₂ * v₃ - u₃ * v₂ | u₃ * v₁ - u₁ * v₃ | u₁ * v₂ - u₂ * v₁ )

= ( 0 - 0 | 0 - 0 | ( 2 - 1 / √ 2 ) * ( - 5 / √ 2 ) - ( - 1 / √ 2 ) * ( 4 - 5 / √ 2 ) )

[ Hier zeigt sich nun, warum eingangs die Wahl der Komponente b₃ = 0 so günstig war: Die beiden ersten Komponenten des Kreuzproduktes sind auf diese Weise einfach zu Null geworden! Anschauliche Erklärung:  Weil die dritten Komponenten von a und b Null sind, liegen sowohl a als auch b und somit auch ihre Linearkombinationen u und v in der x-y-Ebene. Da aber das Kreuzprodukt u x v senkrecht auf u und v steht, liegt es parallel zur z-Achse und daher sind seine ersten beiden Komponenten gleich Null. ]

= ( 0 | 0 | [ - ( 10 / √ 2 ) + ( 5 / 2 ) ] - [ - ( 4 / √ 2 ) + ( 5 / 2 ) ] ) 

= ( 0 | 0 | - ( 10 / √ 2 ) + ( 5 / 2 ) + ( 4 / √ 2 ) - ( 5 / 2 ) )

= ( 0 | 0 | - 6  / √ 2 )

= ( 0 | 0 | - 6 * √ 2 / 2 )

= ( 0 | 0 | - 3 * √ 2 )

Daraus ergbt sich:

| u x v | = √ ( 0 ² + 0 ² + ( - 3 * √ 2 ) ² )

= √ ( 9 * 2 )

= 3 * √ 2

= 4,243 (gerundet)

Das ist der gesuchte Flächeninhalt.

Zur Veranschaulichung noch eine kleine Skizze:

Der Inhalt der blau markierten Fläche (Parallelogramm mit den Seiten u und v ) soll berechnet werden.