Betrag einer Funktion als Graph

Question

was passiert mit einem Graphen einer Funktion, wenn ich den Betrag dieser Funktion nehme? Ich habe mal gehört er wird an der x-Achse gespielt dann dass er an der y-Achse gespiegelt wird. Was stimmt denn?

Answer 1

Hi,

hast Du einen Betrag von Bspw. f(x) = x, als g(x) = |x|, dann ist das eine Spiegelung an der y-Achse. Das muss aber nicht sein. Es wird an der Achse (parallel zur x-Achse) gespiegelt, wo die Funktion den Nullpunkt hat (das gilt für lineare Funktionen).

Wenn man aber an einen Lichtstrahl denkt ist "an der x-Achse gespiegelt" nicht so abwegig und gilt immer, auch wenn das bessere Wort "reflektiert" hieße.

Aber schaus Dir selbst an.

 

 

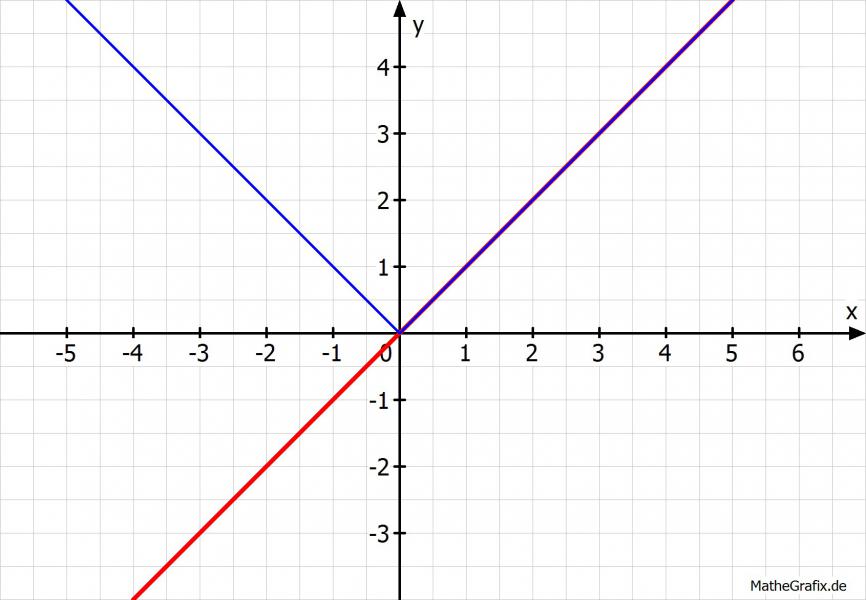
Und für h(x) = x-3, bzw. k(x) = |x-3|

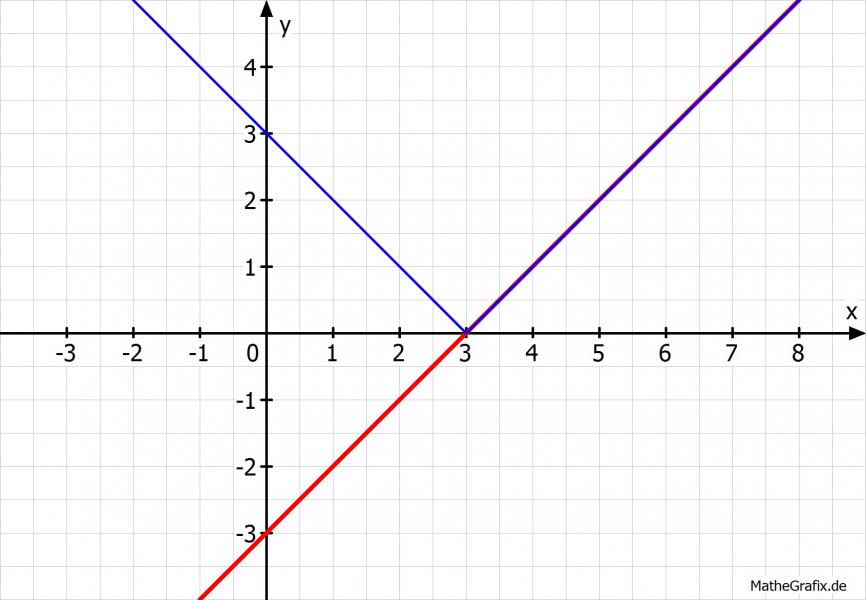
(keine Spiegelung an der y-Achse)

 

Grüße

Comments

Danke :) Und wie ist das bei einer trigonometrischen Funktion?

---

Bedenke, dass bei einem Betrag nicht unterhalb der x-Achse landen kann (solange vor dem Betrag kein negatives Vorzeichen ist). Du hast also im trigonometrischen am Nullpunkt immer Deine Symmetrieachse.

Der Sinus: