Am einfachsten ist es sich eine Vierfeldertafel aufzuschreiben. Die inkl. aller Wahrscheinlichkeiten für die Baumdiagramme siehst du hier
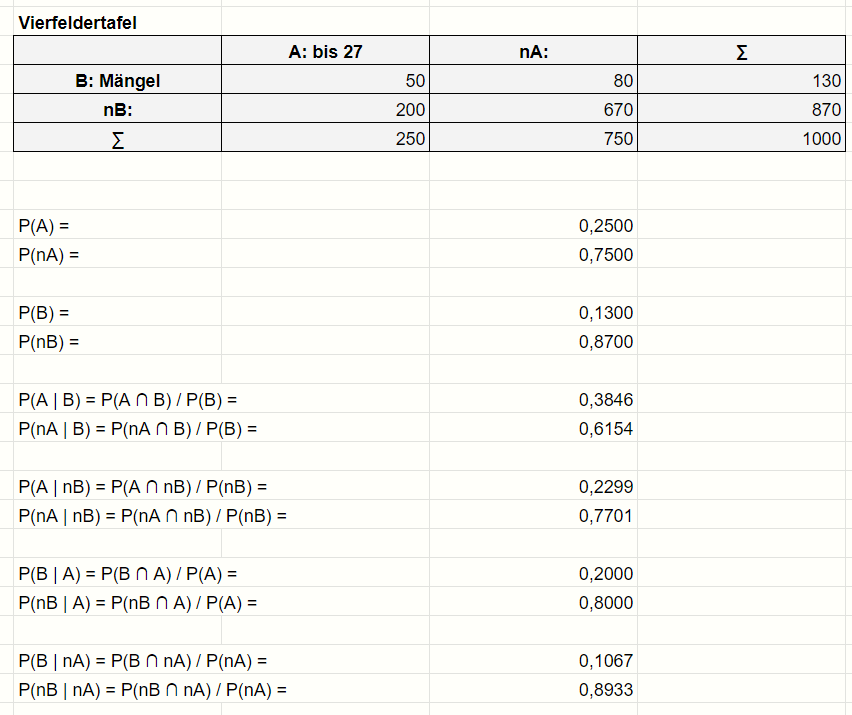
a. Erstellen Sie aus diesem Zusammenhang ein Baumdiagramm.
Wollt ihr das mal probieren?
b. Bestimmen Sie, wie viele mangelhafte Autos die Beamten bei der Kontrolle weiterer 200 Autos erwarten können.
200 * 130/1000 = ...
c. Bestimmen Sie die Wahrscheinlichkeit, dass unter den nächsten 10 Autos mindestens ein mangelhaftes Auto ist.
1 - (1 - 130/1000)^10 = ...