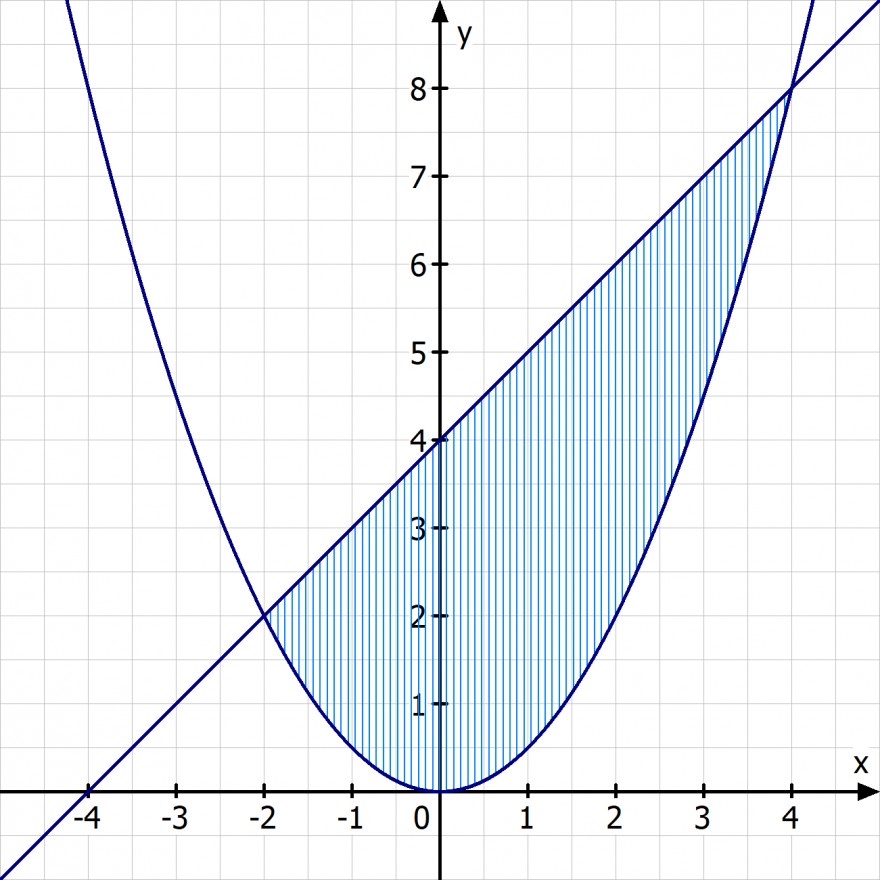
b) Die Graphen der beiden Funktionen f und g umschließen eine Fläche. Berechnen sie deren Inhalt und stellen Sie die Fläche grafisch dar
f(x) = x^2/2 ; g(x) = x + 4
d(x) = f(x) - g(x) = x^2/2 - x - 4
D(x) = x^3/6 - x^2/2 - 4·x
Nullstellen
d(x) = x^2/2 - x - 4 = 0 --> x = -2 ∨ x = 4
∫ (-2 bis 4) d(x) dx = D(4) - D(-2) = (4^3/6 - 4^2/2 - 4·4) - ((-2)^3/6 - (-2)^2/2 - 4·(-2)) = -18 → Die Fläche beträgt 18 FE.