Ich hätte ein paar Fragen und zwar muss ich entscheiden ob diese folgenden Terme gleichwertig sind oder nicht und dann auch noch begründen
Meine Aufgaben&Antworten:
X+X = X×X : NEIN, X+X=2X X×X =X^2
X+X+X = X×X^2 : Ja, weil X+X+X=3X 3×X = 3X
X×X×X=X×X^2: JA, X×X×X= X^3 X×X^2
A^2
Das sind hier die restlichen Aufgaben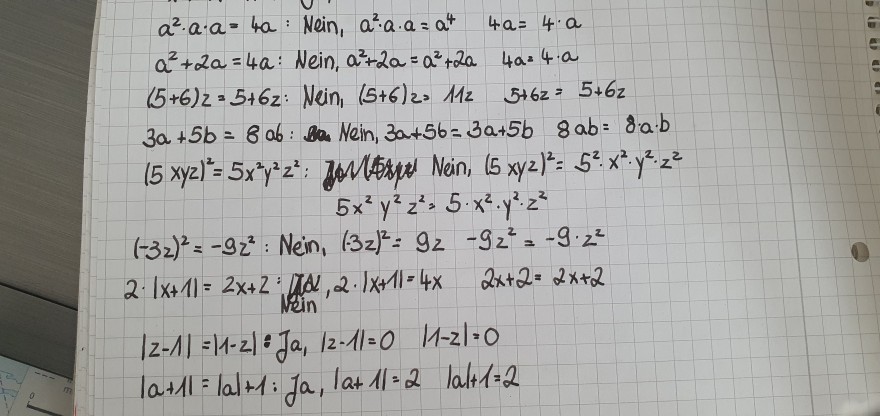
Text erkannt:
\( a^{2} \cdot a \cdot a=4 a: \) Nein, \( a^{2} \cdot a \cdot a=a^{4} \quad 4 a=4 \cdot a \)
\( a^{2}+2 a=4 a: \) Nein, \( a^{2}+2 a=a^{2}+2 a \quad 4 a=4 \cdot a \)
\( (5+6) 2=5+6 z: \) Nein, \( (5+6)=112 \quad 5+6 z=5+6 z \)
\( 3 a+5 b=8 a b: \sin N \operatorname{cin}, 3 a+5 b=3 a+5 b \quad 8 a b=8 a \cdot b \)
\( (5 x y z)^{2}=5 x^{2} y^{2} z^{2}: 70(1+x y+1)(5 x y z)^{2}=5^{2} \cdot x^{2} \cdot y^{2} \cdot z^{2} \)
\( 5 x^{2} y^{2} z^{2}=5 \cdot x^{2} \cdot y^{2} \cdot z^{2} \)
\( (-3 z)^{2}=-9 z^{2}: \operatorname{Nein}_{1}(-3 z)^{2}=9 z-9 z^{2}=-9 \cdot z^{2} \)
\( 2 \cdot|x+1|=2 x+2 ;|\operatorname{JA}| 2 \cdot|x+1|=4 x \quad 2 x+2=2 x+2 \)
\( |z-1|=|1-2|:\{a,|2-1|=0 \quad|1-z|=0 \)
\( |a+1|=|a|+1: f a,|a+1|=2 \quad|a|+1=2 \)
Es wäre sehr hilfreich wenn jemand einfach schreiben würde z.B. 1. Aufgabe: falsch und kurz warum
Danke