Hallo,
setze:$$\nabla f(x,y)=\begin{pmatrix} 4(x-y)^3-14x+18y\\ -4(x-y)^3-14y+18x\end{pmatrix}=\begin{pmatrix} 0\\0 \end{pmatrix}\implies \begin{cases}4(x-y)^3-14x+18y=0 \, \text{(I)} \\ -4(x-y)^3-14y+18x=0 \, \text{(II)} \end{cases}$$ Addierst du die beiden Gleichungen, so ist \(-14x-14y+18y+18x=4x+4y=0\) und damit letztlich \(y=-x\). Setzt du das in (i) ein, so hast du \(4(2x)^3-14x-18x=32x^3-32x=32x(x^2-1)=0\). Insgesamt hast du dann \(x_{1,2}=\pm 1\) und damit die beiden kritischen Punkte \((1,-1)\) und \((-1,1)\). Setzt du \(x=-y\) in (ii) ein, so folgt er letzte kritische Punkt, nämlich \((0,0)\).
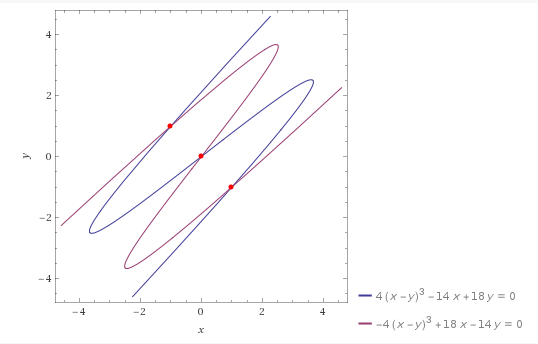
Um diese kritischen Punkte den verschiedenen Begriffen (Maximum, Minimum, Sattelstelle usw.) zuzuordnen, guckst du dir die Definitheit der Hesse-Matrix an. Es gilt:$$H_f(x,y)=\begin{pmatrix} 12(x-y)^2-14 & -12(x-y)^2+18 \\ -12(x-y)^2+18 & 12(x-y)^2-14 \end{pmatrix}$$ und damit \(H_f(0,0)=\begin{pmatrix} -14 & 18 \\ 18 & -14 \end{pmatrix}\). Da wir \(\lambda_1 =4 \) und \(\lambda _2=-32\) als Eigenwerte haben, also positiv und negative, ist \(H_f(0,0)\) indefinit und \((0,0)\) damit ein Sattelpunkt.
Weiter gilt \(H_f(1,-1)=H_f(-1,1)=\begin{pmatrix} 34 & -30 \\ -30 & 34 \end{pmatrix}\). Diese Matrix hat mit \(\lambda_1=4\) und \(\lambda_2=64\) nur positive Eigenwerte (und die Matrix damit positiv definit), damit sind beide Punkte jeweils ein striktes lokales Minimum von \(f\).
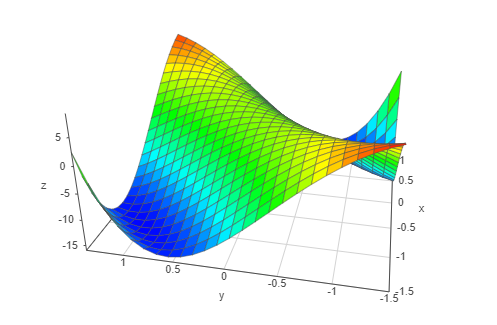
Die Minima siehst du ganz gut an den beiden dunkelblau-eingefärbten Tälern, während der Sattelpunkt genau in der Mitte ist.