Hallo Hanna,
Ich bin schon so weit, dass ich das Gleichungssystem aufgestellt habe:
es ist nicht nötig ein Gleichungssystem aufzustellen, und es ist auch nicht ersichtlich, wie Du darauf gekommen bist.
In einem Parallelogramm halbieren sich die Diagonalen gegenseitig. Ist das Rechteck \(ABCD\) ein Parallelogramm, so liegt der Schnittpunkt \(M\) der Diagonalen bei $$M = \frac 12 (A + C) =\frac 12 \left( \begin{pmatrix}3\\ -1\\ 4\end{pmatrix} + \begin{pmatrix}5\\ 4\\ 2\end{pmatrix} \right) = \begin{pmatrix}4\\ 1.5\\ 3\end{pmatrix}$$Für \(M= (B + D)/2\) muss das identische Ergebnis heraus kommen. Prüfe das bitte nach. Falls nicht, so war es kein Parallelogramm.
Tipp: Zeichne es Dir IMMER auf. Da sich hier die Punkte im 3-dimensionalen befinden, mache einfach 2 Skizzen des Parallelogramms. Zum einen in der XY-Ebene (1. und 2.Koordinate) und zum anderen in der YZ-Ebene (2. und 3. Koordinate)
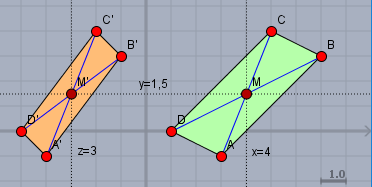
Oben siehst Du das Resultat. Die X-Achse geht nach rechts, die Y-Achse nach oben und die Z-Achse nach links. Das grüne Parallelogramm ist die Projektion in die XY-Ebene und das braune die Projektion in die YZ-Ebene. D.h. ich habe jeweils zwei der drei Koordinaten der Punkte dort eingezeichnet. Dann zeichne die Diagonalen ein und Du kannst das Ergebnis aus der Zeichung ablesen.