Parametrisierung eines Normalgebiets (Mehrdimensionale Integration)

Question

Aufgabe:

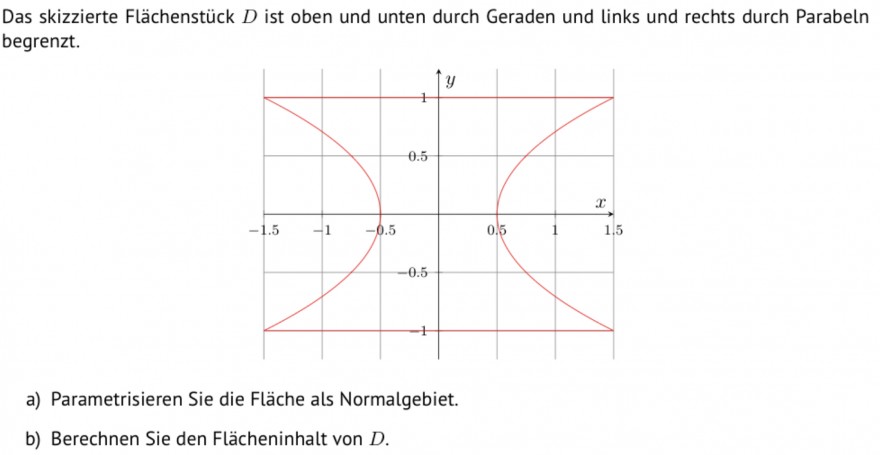
Text erkannt:

Das skizzierte Flächenstück \( D \) ist oben und unten durch Geraden und links und rechts durch Parabeln
begrenzt.
a) Parametrisieren Sie die Fläche als Normalgebiet.
b) Berechnen Sie den Flächeninhalt von \( D \).

Problem/Ansatz:

Ich weiß hier leider überhaupt nicht wie ich anfangen soll.

Eine Funktionsvorschrift oder ähnliches ist hier nicht gegeben, dementsprechend weiß ich nicht, wie ich die Aufgabe angehen soll.

Ich hätte zunächst gedacht, dass ich die Grenzen des Doppelintegrals angeben soll, aber mir fehlt ja die gegebene Funktion.

Man kann z.B sagen, dass x∈ (-1,5 ; 1,5) ist, wie man aber dann das Innere integral abhängig von y findet ohne irgendeinen Hinweis zu besitzen ist mir schleierhaft.

Ich freue mich auf jegliche Unterstützung!

Comments

Ein Ansatz für den Flächeninhalt wäre bestimmt wenn man annimmt dass deine zwei Parabeln durch die Punkte (0.5,0), (-0.5,0) und die 4 weiten Punkte die man erahnen kann verläuft, jetzt könnte man das ganze Bild um 90 Grad drehen die Funktionen aufstellen und das Integral bilden...

Ist nur ein ansatz aber vielleicht hilft es!

LG

---

Also ist hier tatsächlich nur von dem Integral der Fläche gemeint, sogesehen eindimensional?

Die Aufgabe geht dann so weiter

Text erkannt:

c) Berechnen Sie das Flächenträgheitsmoment von \( D \) um die \( x \) -Achse: \( I_{x}=\iint_{D} y^{2} d x d y \)
d) Berechnen Sie das Flächenträgheitsmoment von \( D \) um die \( y \) -Achse: \( I_{y}=\iint_{D} x^{2} d x d y \)

Also zusammengefasst soll man wahrscheinlich zunächst das Integrationsgebiet berechnen, aber welche Grenzen werde ich dann bei den jeweiligen Integralen einsetzen müssen?

---

Ich hätte es jetzt mal so gemacht. Bezeichnet man das jetzt als Parametrisierung?

Answer 1

hallo

du hast doch erstmal -1<=y<=1 und wegen der Randkurven x=y^2+0,5  hast du Grenzen für -y^2-0,5<x<y^2+0,5

aber soweit ich sehe geht auch dein Ansatz; allerdings nur für die Fläche.

Gruß lul

Comments

Das was lul sagt,

Normalgebiet: D = {(x,y)|y ∈ [-1,1], g(y)<= x<= j(y)}

g(y)= -y²-0,5

j(y)=y²+0,5

=> Mit Fubini für Normalgebiete(Die Definition ist in deinen Unterlagen) kannst du jetzt einfach Integrieren.

Lösung für b ist bei mir 10/3

Lösung für c ist bei mir 22/15

Lösung für d ist bei mir 229/210

Alle Angaben ohne Gewähr

Grüße aus K town

---

Vielen Dank euch beiden, dann muss ich auf jedenfall bei der c) und d) nochmal durchrechnen :)