Hallo Lena,
Die Mittelpunkte aller Kreise, die \(g\) berühren, befinden sich auf einer (bzw. zwei) Geraden die mit Abstand \(r=4\text{cm}\) parallel zu \(g\) verläuft. Und die Mittelpunkte aller Kreise mit Radius \(r\), die \(P\) enthalten, befinden sich auf einem Kreis mit Mittelpunkt \(P\) und Radius \(r\).
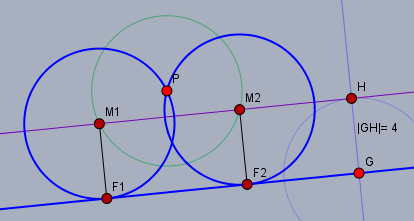
Folglich musst Du nur eine Parallele \(h\) (lila) zu \(g\) im Abstand \(4 \text{cm}\) konstruieren (auf der Seite, auf der \(P\) liegt) und den Kreis \(k_2\) (grün) mit Radius \(r=4\text{cm}\) um \(P\) ziehen. Die Schnittpunkte des Kreises \(k_2\) mit der Parallelen \(h\) sind die Mittelpunkte \(M_1\) und \(M_2\) der gesuchten Kreise.
Fälle von \(M_{1,2}\) das Lot (schwarz) auf \(g\) zum Lotpunkt \(F_{1,2}\). Ziehe jeweils einen Kreis (blau) um \(M_k\) mit dem Radius \(|M_kF_k|\).
Gruß Werner