Problem DGL Musterlösung

Question

Aufgabe

Text erkannt:

\( 11-x^{3} \cdot y+x^{2} \cdot y^{\prime}=-2 x^{3} \)
\( \Leftrightarrow \underset{p(x)}{=x \cdot y+y^{\prime}}=\underbrace{-2 x}_{q(x)} \rightarrow P(x)=-\frac{1}{2} x^{2} \)

Problem/Ansatz:

Hallo, ich habe diese Musterlösung und verstehe an sich auch den Vorgang der Rechnung, mein Problem ist dass ich nicht nachvollziehen kann wieso -xy als mein p(x) übrig bleibt, mit was würde es gekürzt ? Mein q(x) ist nachvollziehbar.

VG Sara

Answer 1

Hallo,

die DGL wurde auf beiden Seiten durch x^2 geteilt.

Man kann auf der linken Seite zuerst x^2 ausklammern und dann teilen.

Comments

Hallo, danke für die Antwort, kannst du mir dies vielleicht vorrechnen wie genau es gemeint ist.

---

-x^3 y +x^2 y'= -2x^3

x^2(-xy +y') = -2x^3 |: x^2 ≠ 0

-xy +y' = -2x

der restliche Weg via Variation der Konstanten :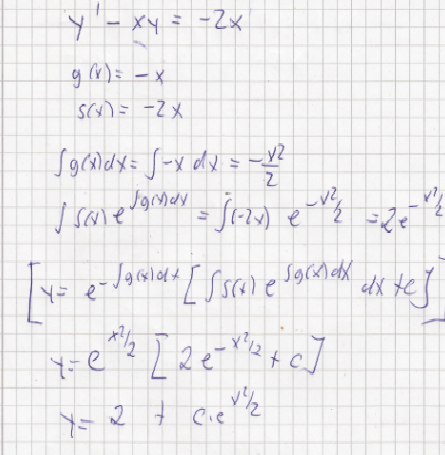

(mit Lösungsformel)

Die Bezeichnungen sind anders , aber vielleicht hilft das trotzdem weiter.

PS: Du kannst die DGL auch via Trennung der Variablen lösen:

(je nachdem , wie die Aufgabe genau lautete)

-xy +y' = -2x | + xy

y'= -2x +xy

dy/dx=x(y-2)

dy/(y-2)= x dx

usw.

---

Vielen Dank, jetzt habe ich es verstanden.