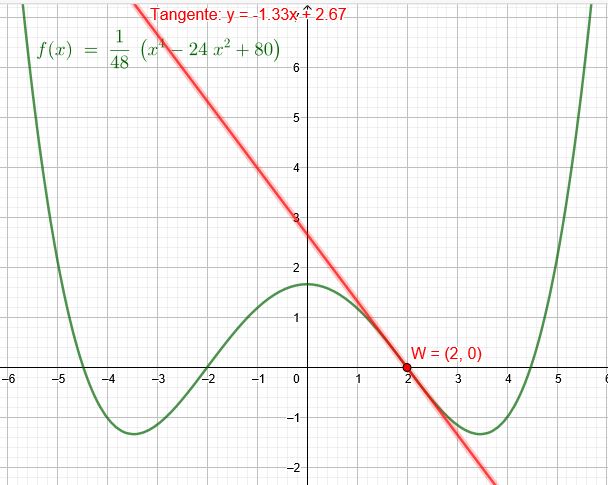
symmetrisch zur y-Achse . In \(P(2|0)\) ist eine Wendetangente mit der Steigung \(m=-\frac{4}{3} \) .
\(P(2|0)\)→\(Q(-2|0)\)
\(f(x)=a(x-2)(x+2)(x-N)(x+N)=a[(x^2-4)(x^2-N^2)]\\=a[x^4-N^2x^2-4x^2+4N^2]\)
Wendetangente mit \(m=-\frac{4}{3} \):
\(f'(x)=a[4x^3-2N^2x-8x]\)
\(f'(2)=a[32-4N^2-16]=-\frac{4}{3}\)
\(a=\frac{1}{3(N^2-4)}\)
\(f'(x)=\frac{1}{3(N^2-4)}[4x^3-2N^2x-8x]\)
\(P(2|...)\) Wendepunkt:
\(f''(x)=\frac{1}{3(N^2-4)}[12x^2-2N^2-8]\)
\(f''(2)=\frac{1}{12(N^2-1)}[40-2N^2]=0\)
\(N^2=20\)
\(a=\frac{1}{48}\)
\(f(x)=\frac{1}{48}[x^4-24x^2+80]\)