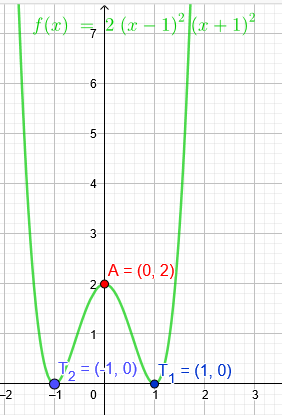
Bestimmen Sie die ganzrationale Funktion 4. Grades, deren Graph
a.) symmetrisch zur y-Achse ist, durch A(0|2) verläuft und den T_1(1|0) und somit T_2(-1|0) hat.
Lösung über die Nullstellenform der Parabel 4.Grades:
f(x)=a*(x-1)^2*(x+1)^2
A(0|2)
f(x)=a*(0-1)^2*(0+1)^2=a
a=2
f(x)=2*(x-1)^2*(x+1)^2