Ermitteln Sie Extrempunkte einer Funktion!

Question

Die Funktion lautet:

f(x)=ax² -2a² x

Und es gelten folgende Regeln:

a<0

x=a

So, ich kann zwar die Ableitungsfunktion erstellen, aber dann komm ich nicht mehr weiter...Freue mich über jede Hilfe

Answer 1

 

Ist wirklich x = a? Dann würde

f(x)=ax² -2a² x

zu

f(x) = x * x² - 2 * x² * x = x³ - 2x³ = -x³

f'(x) = -3x²

f''(x) = -6x

 

Notwendige Bedingung für einen Extrempunkt f'(x) = 0, also x = 0

Hinreichende Bedingung für einen Extrempunkt f''(x) ≠ 0, also f''(0) ≠ 0. f''(0) ist aber -6*0 = 0.

Deshalb würde diese Funktion keinen Extrempunkt haben!

 

f(x) = -x³

 

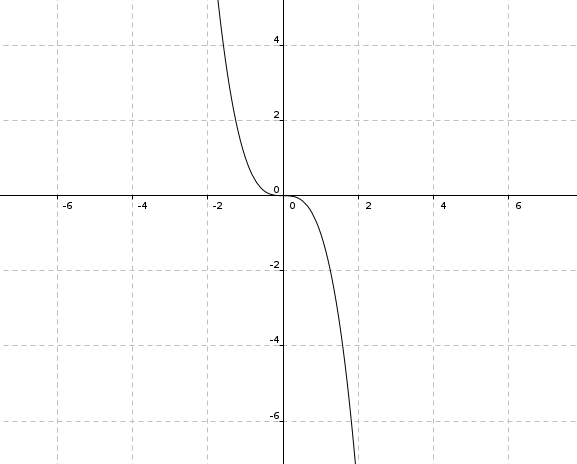
Habe ich da etwas falsch verstanden?

 

Besten Gruß

Answer 2

  f ( x ) = a * x² -2 * a² * x
  f ´ ( x ) = 2ax - 2a^2
  Extrempunkt
  2ax - 2a^2 = 0
  ax = a^2
  x = a
  Die ist bereits die Lösung.

  f ( a ) = a * a^2 - 2 * a^2 * a
  f  ( a ) = a^3 - 2 a^3 = - a^3

  E ( a  l -a^3 )

  mfg Georg