Aufgabe:
$$ \sum \limits_{n=1}^{\infty} \frac{(k!)^2}{2k!} \text{ auf Konvergenz überprüfen } $$
Problem/Ansatz:
Ich habe die Aufgabe bei einer Wikibooks Seite "Mathe für Nichts-Freaks" gefunden und versucht zu lösen.
Hier deren Lösung:
Quotientenkriterium:
$$ \begin{aligned} \left|\frac{a_{k+1}}{a_{k}}\right|=\frac{\frac{((k+1) !)^{2}}{(2 k+2) !}}{\frac{(k !)^{2}}{(2 k) !}}=& \frac{((k+1) !)^{2}(2 k) !}{(k !)^{2}(2 k+2) !}=\frac{k ! k !(k+1)^{2}(2 k) !}{k ! k !(2 k) !(2 k+1)(2 k+2)}=\frac{k^{2}+2 k+1}{4 k^{2}+6 k+2} \\ =& \frac{1+\frac{2}{k}+\frac{1}{k^{2}}}{4+\frac{6}{k}+\frac{2}{k^{2}}} \longrightarrow \frac{1}{4}<1 \end{aligned} $$
Damit konvergiert die Reihe absolut
Meine Lösung: 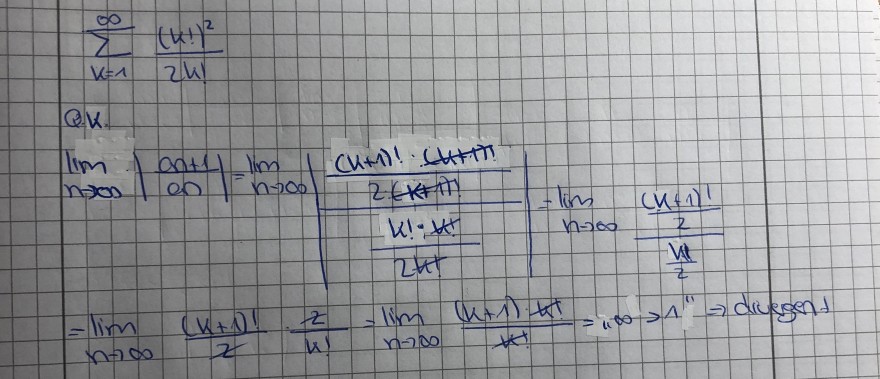
Meine Frage wäre: Warum darf man bei meiner ersten Zeile nicht kürzen? Bzw. Wo habe ich den Fehler gemacht.