Quotientenkriterium: Kürzen beim Binomialkoeffizient

Question

Aufgabe:

$$\sum \limits_{n=1}^{\infty} \frac{(k!)^2}{2k!} \text{ auf Konvergenz überprüfen }$$

Problem/Ansatz:

Ich habe die Aufgabe bei einer Wikibooks Seite "Mathe für Nichts-Freaks" gefunden und versucht zu lösen.

Hier deren Lösung:

Quotientenkriterium:
$$\begin{aligned} \left|\frac{a_{k+1}}{a_{k}}\right|=\frac{\frac{((k+1) !)^{2}}{(2 k+2) !}}{\frac{(k !)^{2}}{(2 k) !}}=& \frac{((k+1) !)^{2}(2 k) !}{(k !)^{2}(2 k+2) !}=\frac{k ! k !(k+1)^{2}(2 k) !}{k ! k !(2 k) !(2 k+1)(2 k+2)}=\frac{k^{2}+2 k+1}{4 k^{2}+6 k+2} \\ =& \frac{1+\frac{2}{k}+\frac{1}{k^{2}}}{4+\frac{6}{k}+\frac{2}{k^{2}}} \longrightarrow \frac{1}{4}<1 \end{aligned}$$
Damit konvergiert die Reihe absolut

Meine Lösung: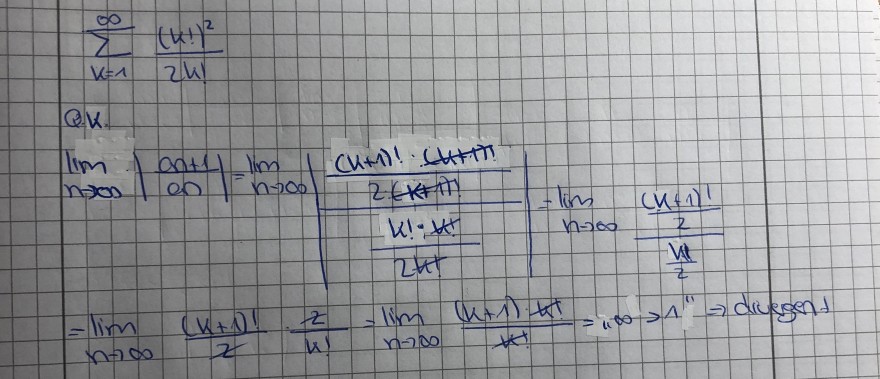

Meine Frage wäre: Warum darf man bei meiner ersten Zeile nicht kürzen? Bzw. Wo habe ich den Fehler gemacht.

Comments

Es ist etwa (k+1)!/k=k, das finde ich bei dir nicht. Weiter hast du bereits am Anfang statt (2k)! einfach 2k! geschrieben, was nicht das gleiche ist. Sodann ist (2(k+1))!/(2k)!=(2k+2)!/(2k)!=(2k+2)*(2k+1), das finde ich bei dir auch nicht.

---

Hallo,

Du hast mit

$$2 \cdot k!= 2 \cdot ( 1 \cdot 2 \cdots k)$$

gerechnet. Die Lösung mit

$$(2k)!=1 \cdot 2 \cdots (2k-1) \cdot 2k$$

Gruß

PS: Kommentare haben sich überschnitten.

---

Vielleicht kannst du noch die Originalaufgabe verlinken?

---

Müsste dann nicht schon in der Aufgabenstellung das in Klammern geschrieben sein?

Weil das kann man ja gar nicht so erkennen, ob das 2k! oder (2k)! mit gemeint ist @MathePeter

---

Hier der Link dazu: https://de.wikibooks.org/wiki/Mathe_für_Nicht-Freaks:_Aufgaben_zu_Ko…

---

Die Klammern hätten auch in der Aufgabenstellung stehen müssen.

ps: Aber dort (Reihe 2) stehen ja auch Klammern.

---

Ist doch in der Aufgabenstellung mit Klammern geschrieben?

---

Ok, ich seh's gerade auch, hab verpennt :D Sorry! Und Danke an alle!

Answer 1

(2k)!≠2k! und (2k+2)!≠2(k+1)!

Comments

Ja, aber woran soll ich das denn erkennen, dass da geklammert sein soll? Also aus der Aufgabenstellung her

---

Habe den Fehler gefunden, habe die Aufgabe falsch abgeschrieben, trotzdem

---

Hallo,

ich habe da mal eine Frage: Was ist eigentlich der Sinn davon, eine Antwort die bereits zweimal gegeben ist, noch ein 3. Mal zu geben?

Gruß