Hallo,
Dass ... $$x = r \cdot \cos \varphi \\ y = r \cdot \sin \varphi$$... ist, das weißt Du! Dann setzte einfach das \(r(\varphi)\) aus der Aufgabe ein und leite \(x\) und \(y\) nach \(\varphi\) ab:$$\begin{aligned} \frac{\partial x}{ \partial \varphi } &= 2 \cos(2 \varphi )\cos \varphi - \sin(2 \varphi) \sin \varphi \\ &= 2 \left( \cos^2 \varphi - \sin^2 \varphi\right) \cos \varphi - 2\sin^2\varphi \cos \varphi \\ &= 2 \cos \varphi \left( \cos^2 \varphi - 2\sin^2\varphi \right) \\ &= 2 \cos \varphi \left( 3\cos^2 \varphi - 2\right)\\ \frac{\partial y}{ \partial \varphi } &= 2 \cos(2 \varphi )\sin \varphi + \sin(2 \varphi) \cos \varphi \\ &= 2 \left( \cos^2 \varphi - \sin^2 \varphi\right)\sin \varphi + 2\sin\varphi \cos^2 \varphi \\ &= 2 \sin \varphi\left( 3\cos^2 \varphi - \sin^2 \varphi \right) \\ &= 2 \sin \varphi\left( 4\cos^2 \varphi - 1 \right) \end{aligned}$$Damit ist der Tangentialvektor $$\partial \begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}\cos \varphi \left( 3\cos^2 \varphi - 2\right)\\ \sin \varphi\left( 4\cos^2 \varphi - 1 \right)\end{pmatrix}$$Die Funktion sieht aus wie ein vierblättriges Kleeblatt
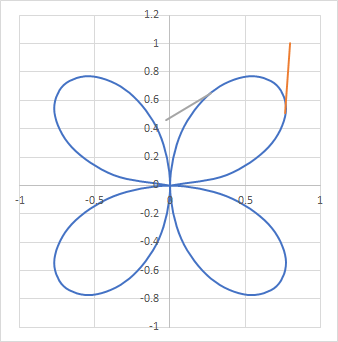
Die zwei Striche sind zwei Tangentialvektoren, die ich zur Probe eingezeichnet habe.
Die Fläche der Figur ist die Fläche der vier Blätter. Ein Blatt wird durch den Durchlauf von \(\varphi \in [0; \pi/2]\) gebildet. Also ist die Gesamtfläche$$\begin{aligned} F &= 4 \int_0^{\pi/2} \frac {r^2}2 \, \text d\varphi \\ &= 2 \int_0^{\pi/2} \sin^2 (2 \varphi) \, \text d \varphi \\ &= 2 \left( \left. \frac 18 \left( 4 \varphi - \sin (4 \varphi )\right) \right|_0^{\pi/2} \right) \\ & = \frac \pi 2\end{aligned}$$ zu dem Integral siehe auch 'Kreissektor'.