Was macht Deine wissenschaftliche Seminararbeit?
Soll das dazu passen?
Graph des Polynoms bis a=1 aufziehen
Graph schneidet Ursprung
φ aufziehen und Pz möglichst genau in Ursprung plazieren
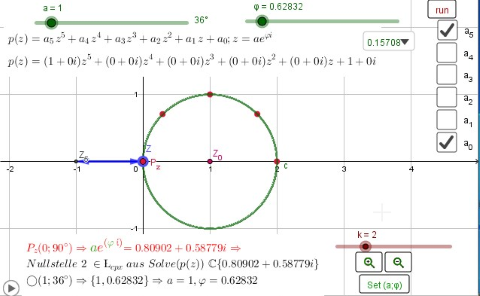
(a,φ) Polarkoordinaten der Nullstelle - rote Zeile Umrechnung aucf komplexe Zahl und vergleich mit numerischer Berechnung. φ weiter aufziehen 2. Umlauf - einmal rum und wieder möglichst genau in Ursprung stellen:
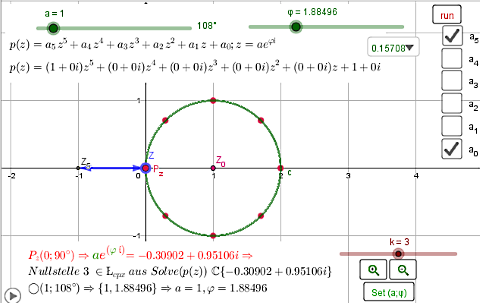
3. Umlauf

die restlichen beiden Umläufe spar ich mir ....
Du hast Dein Polynom ja seeehr vereinfacht?
Kartesische Koordinaten \( x, y \)
$$ \begin{array}{l} x=r \cos \varphi(\text { Realteil von } z) \\ y=r \sin \varphi(\text { Imaginärteil von } z) \end{array} $$
Polare Koordinaten \( r, \phi \)
Betrag \( r=|z|=\sqrt{x^{2}+y^{2}} \)
Argument arg \( (z):=\phi \) ergibt sich aus \( \tan \varphi=\frac{y}{x} \) Quadrant beachten!