Text erkannt:
(7.1)
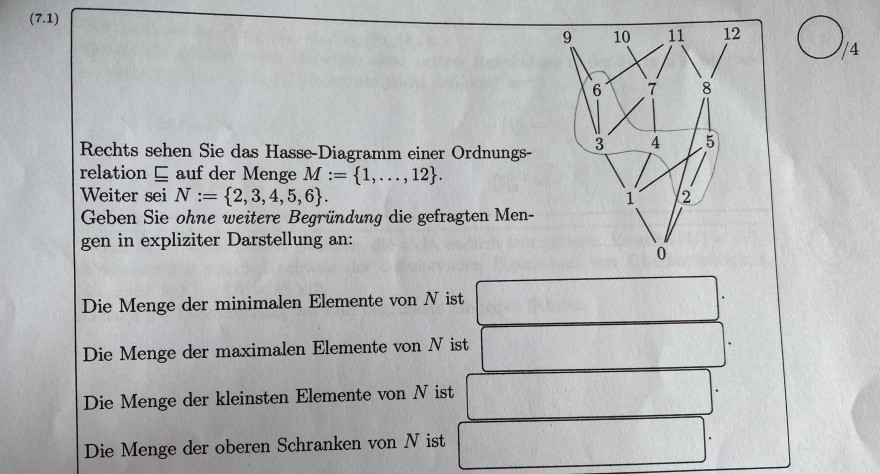
Weiter sei \( N:=\{2,3,4,5,6\} \)
gen in expliziter Darstellung an:
relation \( \sqsubseteq \) auf der Menge \( M:=\{1, \ldots, 12\} \). Rechts sehen Sie das Hasse-Diagramm einer Ordnungs-
Geben Sie ohne weitere Begründung die gefragten Men-
Die Menge der minimalen Elemente von \( N \) ist
Die Menge der maximalen Elemente von
Die Menge der kleinsten Elemente von \( N \)
Die Menge der oberen Schranken von \( N \)
Kann mir jemand bitte erklären wie man auf diese Werte kommt? Also wie man diese Elemente bestimmt. Ganz einfach erklären wie man hier an diesem Beispiel vorgeht bitte.
Vielen Dank!