HALLO
erstmal solltest du verstehen, was du da machst. Du kennst den Funktionswert bei 1, du willst ihn bei 1+0,2. Statt auf der Kurve f(x) 0,2 nach rechts zu laufen gehst du in Richtung der Tangente 0,2 weiter, wie in meiner Zeichnung,
also rechnest du; f(1)+f'(1)*0,2 Wert bei 1 und dann mit der Tangentensteigung bei 1 0,2 weiter
f'(1)=1/1-1/(2*√1)=1/2
irgendwo steht da Unsinn; dx=1/2dx ist sicher falsch, gemeint war wohl df=1/2dx wegen df=f'*dx
in deinem Schrieb wird dx für das endliche Δx verwendet entsprechend Δf
also hast du am Ende f(1)=0-1=-1, dx=0,2 , df=f'(1)*dx=1/2*0,2=0,1 und endlich f(1,2)≈-1+0,1=-0,9
am Graphen kannst du das auch sehen.
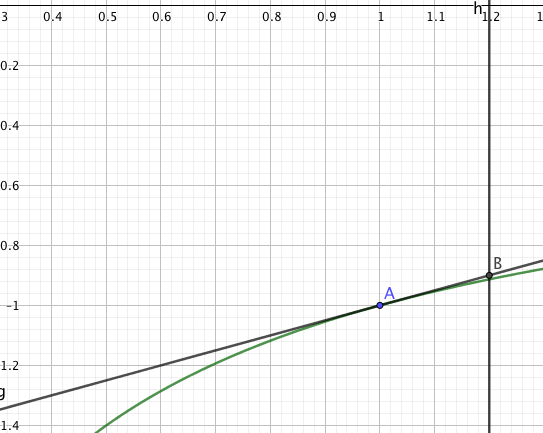
Gruß lul