Hallo,
f''(x) < 0 ⇒ Der Graph ist rechtsgekrümmt
f''(x) > 0 ⇒ Der Graph ist linksgekrümmt
Wie in deiner Aufgabe zuvor, berechnest du zunächst den/die Wendepunkte mit f''(x) = 0.
Bei diesem Graphen sind es zwei Wendepunkte. WP1 (-1|-5), WP2 (1|-5).
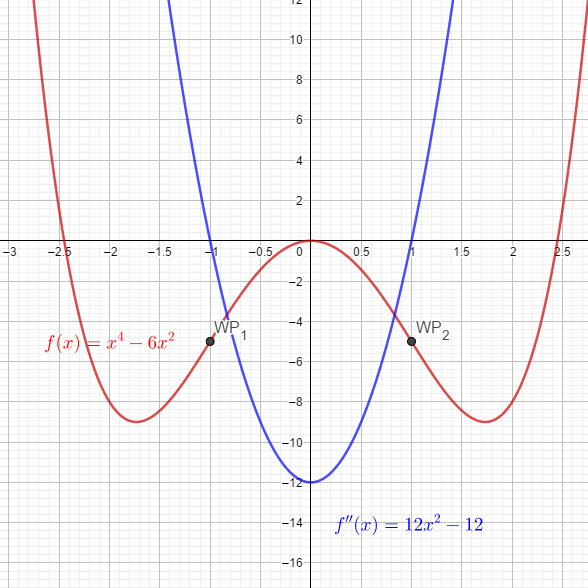
Schau dir den Graphen von f(x) von oben an und stelle dir vor, du würdest mit dem Fahrrad die Strecke entlangfahren. Du musst die ganze Zeit nach links lenken, bis du an dem ersten Wendepunkt angekommen bist. Ab da geht es nach rechts...
Die y-Werte von f''(x) wechseln an der Stelle von WP1 das Vorzeichen, sie gehen von negativ nach positiv. Also ist der Graph im Intervall von -∞ bis -1 linksgekrümmt, im Intervall von 1- bis 1 ist er rechtsgekrümmt, von 1 bis ∞ wieder linksgekrümmt.
Melde dich, wenn du noch Fragen hast.
Gruß, Silvia