|3x-5| = 2 |2x+1| Lösungsmenge bestimmen (Rechenweg vorhanden, bloß verstehe ich eine Lösung nicht) ACHTUNG: gelöst

Question

Aufgabe:

|3x-5| = 2 |2x+1| Lösungsmenge bestimmen (Rechenweg vorhanden, bloß verstehe ich eine Lösung nicht) ACHTUNG: gelöst

B = { x : |3x-5| = 2|2x+1| }

Problem/Ansatz:

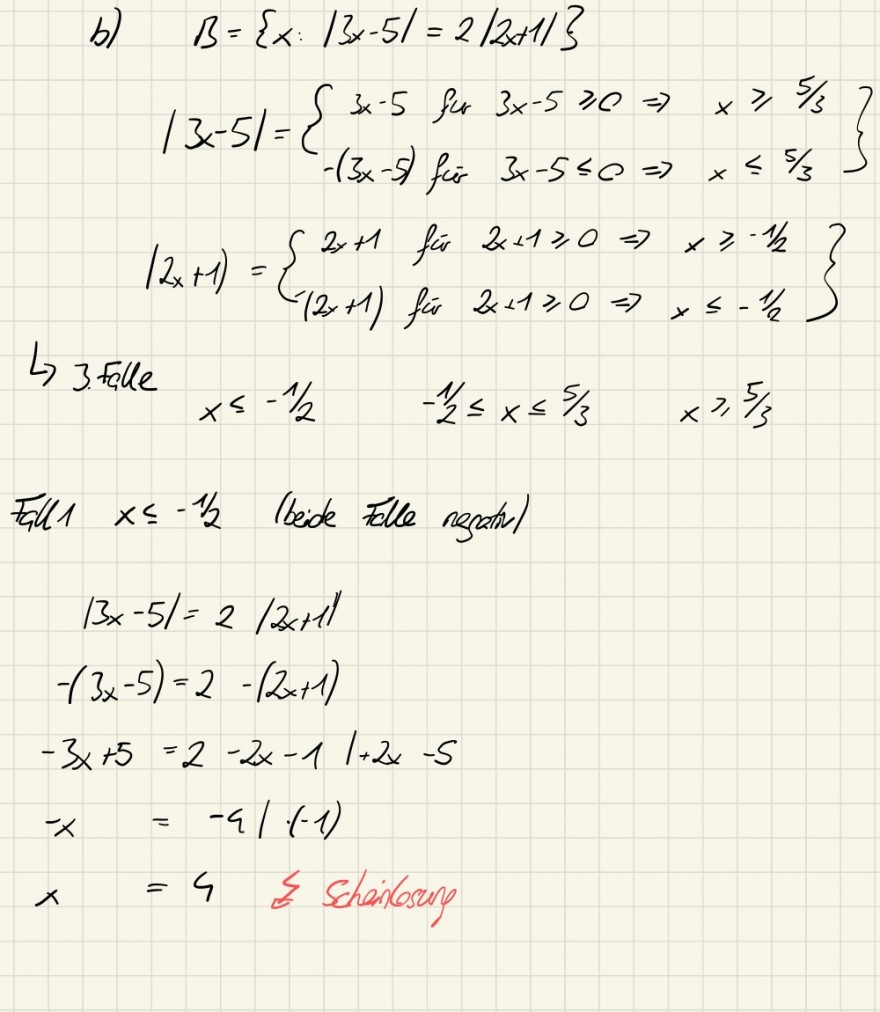
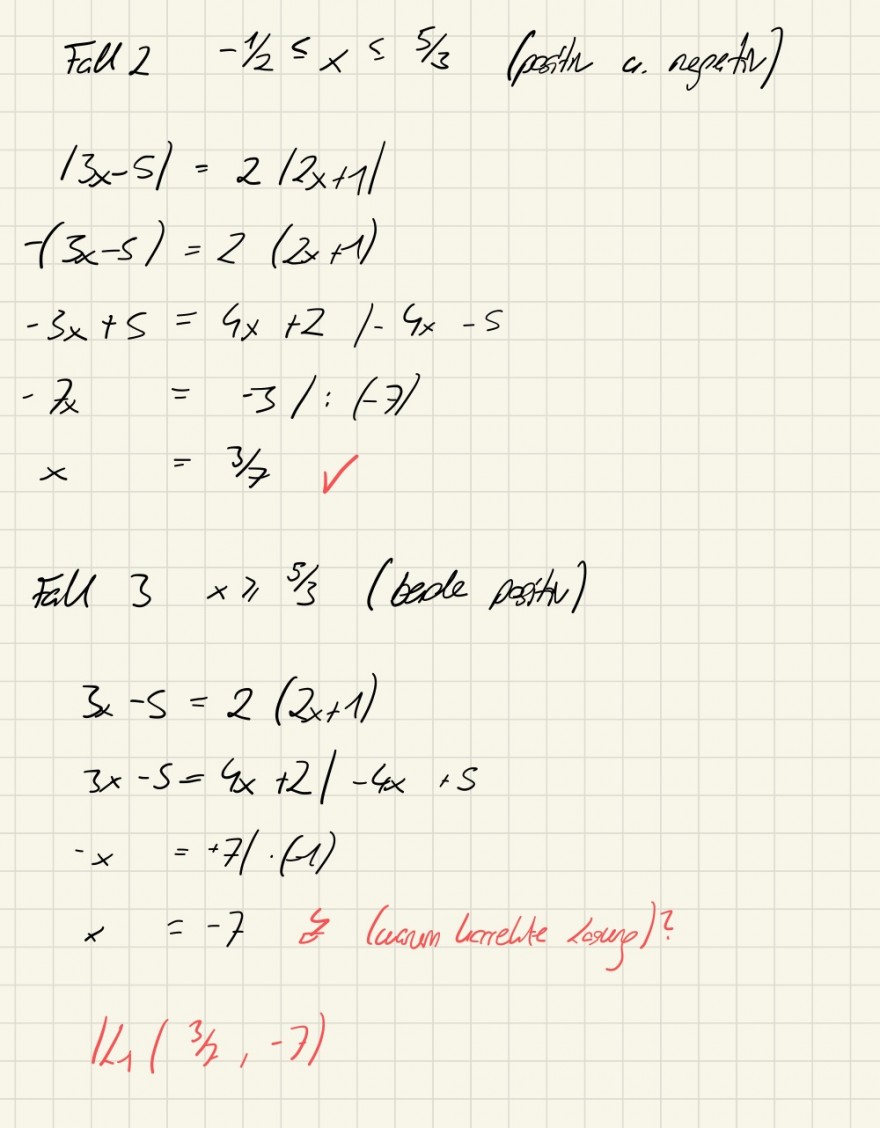
Meine Professorin hat leider nur die Lösung angegeben und ich versteh nicht genau, warum -7 eine Lösung darstellt?

Comments

EDIT: Habe aus deinem Kommentar ausnahmsweise eine Antwort gemacht. Damit dort bei Bedarf separat diskutiert werden kann. Du kannst via "bearbeiten" aus deiner Antwort wieder einen Kommentar machen (zur Frage oder zu einer der Antworten).

---

Fall 1:

4 ist keine Scheinlösung, sondern scheidet als Lösung sofort aus, weil die Bedingung ist: x<=-1/2

Scheinlösungen ergeben sich meist durch Quadrieren.

vgl:

https://www.matheretter.de/wiki/wurzelgleichungen-scheinlosungen-2

Answer 1

Wenn du beide Seiten als Funktionsterme auffasst und graphisch darstellst, siehst du, dass -7 und 3/7 die gesuchten Lösungen sind.

:-)

PS: Bei Fall 1 muss die 2 ein Faktor sein. Daher ergibt dieser Fall x =-7, während Fall 3 keine Lösung liefert.

Answer 2

Okay mein Fehler -7 in die Gleichung eingesetzt und aufgelöst ist Korrekt.

Ich dachte solange die Zahl dem Fall nicht entspricht (in dem Fall der Fall 3) ist die Lösung automatisch nicht korrekt!

Ich muss mir angewöhnen die Probe zu machen!

Comments

Dein erster Fall ist falsch aufgelöst.

---

Bei Fall 1 fehlt in der zweiten Zeile eine Klammer um  -(2x+1)  also ( -(2x+1) ).

In der Zeile danach ist dann gleich schon ein Folgefehler passiert.

---

Das Stimmt leider nicht, die Klammern sind richtig gesetzt.

Fall 1 ergibt 4 die jedoch nicht zur Lösungsmenge gezählt werden kann, da Sie mit dem Fall 1 nicht übereinstimmt

---

Dieser Teil enthält den Klammerfehler:

Ich wiederhole: in Zeile 2 ist bereits ein Fehler. Du tust so, als wäre zu Beginn in der Betragsgleichung rechts ein Plus vor dem Betrag.

Answer 3

-7 ist Lösung der Gleichung 3x-5=2(2x+1).

Solange die Zahl dem Fall nicht entspricht, ist das keine Lösung im Fall 3. Kann aber Lösung in einem anderen Fall sein.

Comments

Beides falsch.

---

Darf somit -7 in der Lösungsmenge auftauchen oder nicht ?

Die Aufgabenstellung ist nämlich -> Geben Sie die Menge in aufzählender Schreibweise an

B = { x : |3x-5| = 2|2x+1| }

---

Wie man relativ leicht nachrechnet ist -7 eine Lösung der Betragsgleichung. Warum Roland das Gegenteil behauptet bleibt wie so oft rätselhaft.

Answer 4

|3x-5| = 2* |2x+1|

sqrt((3x-5)^2) = 2* sqrt((2x+1)^2)   |^2

(3x-5)^2=4*(2x+1)^2

(3x-5)^2-4*(2x+1)^2=0

[(3x-5)+2*(2x+1)]*[(3x-5)-2*(2x+1)]=0

[3x-5+4x+2]*[3x-5-4x-2]=0

[7x-3]*[-x-7]=0

1.) 7x-3=0 ->->  x=3/7

2.) -x-7=0 ->->  x=-7

Probe: 1.)  x=3/7

|3*3/7-5| =  2* |2*3/7+1|

|-26/7|= 2* |13/7| ->-> stimmt

Probe: 2.)  x=-7

|3*(-7)-5| =  2* |2*(-7)+1|

|-26| =  2* |-13| ->-> stimmt auch