Aufgabe:
Wie bezeichnet man eigentlich eine Strecke, welche einfach zu einem Kreis gezogen ist oder auf ihn trifft, ohne ihn zu schneiden, und auch nicht Tangente ist.
Problem/Ansatz:
Also das Problem ist vielleicht mehr historischer Natur(nomen est omen) und rührt aus einem alten Scholion her.
Beispiel:
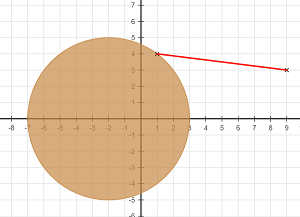
Bei Euklid sind gerade Linien Strecken, die beliebig beidseitig verlängerbar sind, aber keine Geraden im heutigen Sinne.
Ich muß vielleicht dazu sagen, daß ich kein studierter Mathematiker bin, sondern eigentlich studierter Gräzist und mich seit Jahren nur mit altgriechischer Mathematik befasse, insbesondere Euklids Elementen.
Für Tangente verwendet er ephaptomai, aber auch aptomai ἐφάπτομαι, ἅπτομαι. (dies findet sich auch insbesondere bei Archimedes), das erstere ist also lediglich ein Kompositum, und ein Scholiast, als ein Kommentator, versucht nun die Unterscheidung, dass er bei der roten Linie von aptomai (apto) spricht.
Also ich will jetzt hier nicht zu sehr ausschweifen, aber es geht mir dabei noch um was Anderes.
Bei der Winkeldefinition und insbesondere im Rahmen der Raumgeometrie findet sich das Wort auch, also daß zwei Strecken „sich berühren“, wenn sie einen Schnittpunkt mit ihren Endpunkten bilden. Allerdings geht es im griechischen Text auch durcheinander und es wird von Schnittpunkt und nicht von Berührpunkt gesprochen, der ja auch ein Schnittpunkt ist. Um es kurz zu sagen, ich will den Text verwenden und dafür muß man m.E. da im Griechischen einiges ändern. Das ganze ist auch nur eine Sammlung.
Na ja, ich will jetzt hier nicht zu viel sicher sachfremdes schreiben. Die Antworten haben mir schon geholfen. D.h. ich denke auch, daß das einfach irgendeine an den Kreis gezogene Strecke ist, für die es wohl keine besondere Bezeichnung gibt. Allerdings bricht sich daran ja ein bißchen die Unterscheidung: Tangente = 1 Schnittpunkt, Sekante = 2. Daß nur eine Sekante den Kreis schneidet, liegt wohl daran, daß nur dann die Kreislinie vollständig geschnitten wird?