Ich gehe davon aus, dass georgborn mit seiner Vermutung bzgl. des ersten Tiefenwinkels recht hat, dieser also tatsächlich 48,43° misst.
Zunächst eine Skizze:
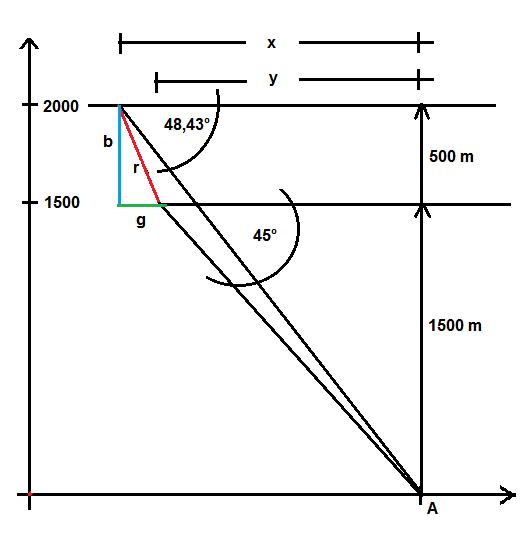
In der fraglichen Minute hat das Flugzeug die rot gezeichnete Strecke zurückgelegt.
Diese ergibt sich mit dem Satz des Pythagoras aus der Höhendifferenz von 500 m (blaue Strecke) und der horizontalen Differenz x - y (grüne Strecke).
Berechnung der grünen Strecke g:
Es gilt:
tan ( 48,43 ) = 2000 / x <=> x = 2000 / tan ( 48,43 ) = 1773,8 m (gerundet)
tan ( 45 ) = 1500 / y <=> y = 1500 / tan ( 45 ) = 1500 m
=> g = x - y = 1773,8 m - 1500 m = 273,8 m
Berechnung der roten Strecke r:
r = √ ( 273,8 2 + 500 2 ) = 570,1 m (gerundet)
Das Flugzeug hat also in der fraglichen Minute 570,1 Meter zurückgelegt, das entspricht einer Durchschnittsgeschwindigkeit v von
v = 570,1 m/min = 34206 m/h = 34,2 km/h
... und ist für ein Flugzeug eigentlich viel zu langsam. Möglicherweise stimmen einige der angegebenen Daten nicht ...?