Hallo Roland,
normalerweise sollte man die Aufgabe mit Hilfe des Strahlensatzes sofort lösen können. Hat aber bis jetzt nur hj gezeigt (Monty kam erst jetzt ...). ich habe noch einen Beweis, der gänzlich ohne Algebra auskommt.
Dafür zunächst eine Behauptung.

Haben zwei seitenparallele Rechtecke, die eine gemeinsame Ecke \(C\) in der hier gezeigten Art & Weise besitzen, beide den gleichen Flächeninhalt, so liegt der gemeinsame Eckpunkt auf der Diagonalen \(TS\) des umhüllenden Rechtecks (hier \(ASFT\)).
Der Beweis läuft über einen Widerspruchsbeweis: angenommen \(C\) liegt nicht auf der Diagonalen \(TS\).
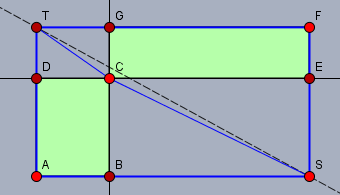
So ist trotzdem das Dreieck \(\triangle DCT\) kongruent zu \(\triangle TCG\) und das Dreieck \(\triangle BSC\) kongruent zu \(CSE\). Zusammen mit der Voraussetzung, dass die beiden Rechtecke \(ABCD\) und \(CEFG\) flächengleich sein sollen, heißt das, dass die Vierecke \(ASCT\) und \(SFTC\) ebenfalls flächengleich sein müssen. Dies kann aber nicht sein, da die Fläche des Dreiecks \(\triangle CST\) nicht leer ist, wenn \(C\) nicht auf der Diagonalen \(TS\) liegt \(\to\) Widerspruch.
Mit diesem Werkzeug ausgerüstet, kann man nun die Gleichheit der Flächen der beiden Parallelogramme zeigen:
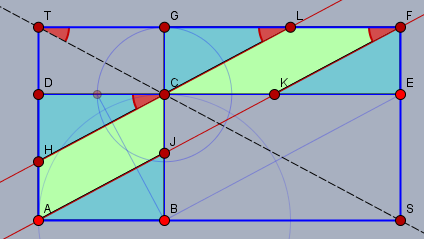
Da \(C\) auf der Diagonalen \(TS\) liegt, müssen aus Gründen der Symmetrie auch die Winkel \(\angle STF\) und \(\angle TFA\) (beide rot) gleich sein. Wegen der Parallelen durch \(AF\) und \(HL\) (rot) gilt das auch für die Winkel \(\angle HCD\) und \(\angle GLC\) - damit sind alle rot markierten Winkel gleich groß. Folglich sind auch die Dreiecke \(\triangle TCG\) und \(\triangle CLG\) kongruent. Gleiches gilt für \(\triangle TCG\) und \(\triangle HCD\). Weiter sind auch wegen der Punktsymmetrie im Parallelogramm die Dreiecke \(\triangle ABJ\) und \(\triangle HCD\) kongruent und die Dreiecke \(\triangle CLG\) und \(\triangle KEF\) ebenso. Folglich sind alle hellblau markierten Dreiecke gleich groß.
Und wenn von der identischen Fläche der beiden Rechtecke \(ABCD\) und \(CEFG\) zweimal die gleiche Dreiecksfläche 'abgeschnitten' wird, so müssen die verbleibenden Flächenstücke gleich groß sein - hier die Parallelogramme \(AJCH\) und \(CKFL\).
Der aufmerksame Leser hat vielleicht bemerkt, dass ich von der Vorgabe, dass \(ABCD\) ein Quadrat sein soll, gar keinen Gebrauch gemacht habe. Das ist auch nicht nötig! Obiges gilt auch, wenn \(ABCD\) ein beliebiges Rechteck ist.