Bei einer Lottoziehung aus 49 Kugeln trägt die erste gezogene Kugel eine gerade Zahl.
Mit welcher Wahrscheinlichkeit ist sie durch 5 teilbar?
Ich muss es mithilfe eines Baumdiagramms lösen.
Ohne hätte ich einfach gesagt, dass es nur 4 Zahlen gibt, die gleichzeitig durch 5 teilbar und gerade sind, nämlich 10 20 30 und 40.
Mit meinem Baumdiagramm komme ich aber nicht auf das Antwort.
Ich würde mich freuen, wenn mir jemand helfen könnte, mein Baumdiagramm zu verbessern.
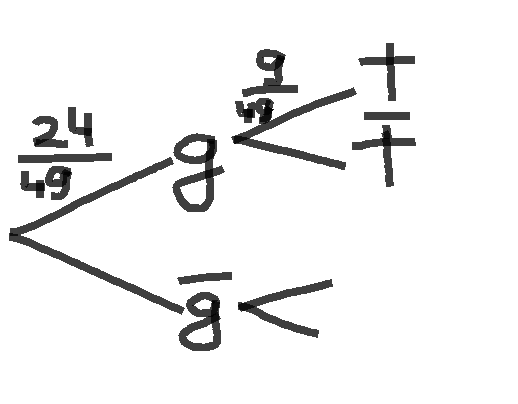
meine Gedanken dabei waren, dass die Zahl entweder gerade oder ungerade ist. Da es gesagt wird, dass die 1. gerade ist, betrachten wir nur den oberen Teil. Die Zahl kann dann entweder durch 5 teilbar sein oder nicht; es gibt insgesamt 9 Zahlen, die durch 5 teilbar sind, nämlich 5,10,15,20,25,30,35,40,45; => 9/45
wenn ich 24/49 mit 6/49 aber multipliziere, komme ich nicht auf was Realistisches.
Alternativ könnte man bei den Teilbaren direkt 4 sagen, weil man ja NUR die geraden betrachtet; aber wenn ich dort direkt 4 schreibe habe ich dann keine Rechnung und der Baum würde auch nicht wirklich stimmen, oder?
wie könnte ich es sonst machen?