Berechne das Integral mit der Trapezformel

Question

Ich habe erneut eine Aufgabe, bei der ich immense Probleme habe. Ich weiß nicht wie ich folgende Aufgabe lösen soll und diese Aufgabe war eine Klausuraufgabe aus dem Jahr 2012, deshalb sollte ich sie gut beherrschen. Ich hoffe, dass mir da jemand helfen kann. Nun hier ist die Aufgabe: 

Berechnen Sie das Integral  ∫(13,0 sind Integralgrenzen)   (x+3exp( -x^2)) dx mit der Trapezformel näherungsweise für n=5 Streifen. Rechnen Sie bei jeder Aufgabe mit mindestens 4 (vier) Nachkommastellen.

a) Der erste Randstützwert für k=0 lautet y0=...  (es soll nach Lösung y0= 3 +-0,001 herauskommen)

b) Der Stützwert für k=1 lautet: y1=...  (es soll nach Lösung y1= 2,603478 +-0,001 rauskommen)

c) Der Stützwert für k=2 lautet: y2=...  (es soll nach Lösung y2= 5,2  +-0,001 rauskommen)

d) Der Stützwert für k=3 lautet: y3=...  (es soll nach Lösung y3= 7,8  +-0,001 rauskommen)

e) Der Stützwert für k=4 lautet: y4=...  (es soll nach Lösung y4= 10,4  +-0,001 rauskommen)

f) Der zweite Randstützwert für k=5 lautet: y5=...  (es soll nach Lösung y5= 13 +-0,001 rauskommen)

g) Mit der Trapezformel erhalten wir den Näherungswert für das Integral:....  (für das Integral soll der Wert 88,409042  +-0,001 rauskommen).

Der Flächeninhalt von einem Trapez ist: A = (a + c ) : 2 · h .  Aber ich weiß nicht was ich jetzt genau berechnen muss.

MfG

Comments

hallo

die funktion, die integriert werden soll, sieht die so x + 3*e^{-x^2} aus?

und die grenzen sind von x=0 bis x=13, richtig?

---

Ja genau das ist sie. Grenzen sind x= 0 bis x= 13 :)

---

Wie würde der näherungswert von ln(2) bestimmt werden mit der trapezform?   Danke für jegliche Hilfe.

Answer 1

hallo

integrationsgrenzen von 0 bis 13 in 5 streifen teilen:
13/5 = 2.6
die schrittweite ist also h = 2.6

das ergibt 6 stützpunkte

y1 = 0 + 3*e^{-0^2} = 3
y2 = 2.6 + 3*e^{-2.6^2} = 2.603478
y3 = 5.2 + 3*e^{-5.2^2} = 5.2
y4 = 7.8 + 3*e^{-7.8^2} = 7.8
y5 = 10.4 + 3*e^{-10.4^2} = 10.4
y6 = 13 + 3*e^{-13^2} = 13

und 5 trapeze, deren flächeninhalte zu berechnen und zu summieren sind

A1 = (y1 + y2)/2 * h = (3 + 2.603478)/2 * 2.6
A1 = 7.2845214 FE

A2 = (y2 + y3)/2 * h = (2.603478 + 5.2)/2 * 2.6
A2 = 10.1445214

A3 = (y3 + y4)/2 * h = (5.2 + 7.8)/2 * 2.6
A3 = 16.9 FE

A4 = (y4 + y5)/2 * h = (7.8 + 10.4)/2 * 2.6
A4 = 23.66 FE

A5 = (y5 + y6)/2 * h = (10.4 + 13)/2 * 2.6
A5 = 30.42 FE

der gesuchte flächeninhalt ist
A = A1 + A2 + A3 + A4 + A5
A = 7.2845214 + 10.1445214 + 16.9 + 23.66 + 30.42
A = 88.4090428 FE

zur info: der genaue(re) wert, nummerisch berechnet ist A = 87.16 FE
 

p.s.

die rechnung lässt sich noch vereinfachen:

A = (y1 + y2)/2 * h + (y2 + y3)/2 + (y3 + y4)/2 * h + (y4 + y5)/2 * h + (y5 + y6)/2 * h
A =  ((y1 + y2) + (y2 + y3) + (y3 + y4) + (y4 + y5) (y5 + y6)) * h/2
A =  (y1 + y2 + y2 + y3 + y3 + y4 + y4 + y5 + y5 + y6) * h/2
A =  (y1 + 2y2 + 2y3 + 2y4 + 2y5 + y6) * h/2

 

gruß
gorgar




 

Comments

@ gorgar:

GeoGebra auf einer Linux-Version?

Ich bin nicht allein :-)

---

Danke für die ausführliche Rechnung das hätte ich ohne Hilfe kaum hinbekommen. Bei Integralaufgaben denke ich direkt immer an Stammfunktion bilden und Grenzen einsetzen. Diesmal war es doch anders. :)

---

Hi Brucy! :-)

Ja, die Grafik ist mit GeoGebra erstellt :-)

Wegen meinen Eltern muss ich mich mit Windows 8 herumplagen, ansonsten wäre ich schon längst auf Linux umgestiegen. Eine Möglichkeit wäre noch Linux parallel zu installieren, aber dafür ist meine SSD zu klein. Vielleicht wäre Platz genug, wenn ich die Platte aufräumen würde ...

Naja, früher oder später wird der Umstieg sicher kommen!

---

@Anonym: hab ich gern gemacht!

Ja, so einfach kann Integralrechnung sein - lässt sich auf die Berechnung von Trapez-Flächeninhalten reduzieren. :P

---

Hallo gorgar,

ich hoffe, dass Du irgendwann die Möglichkeit hast, auf Linux - ich nutze die Distribution Ubuntu - umzusteigen:

Schnell, sicher (für Hacker lohnt es sich kaum, Malware zu entwickeln, da die meisten User noch Windows nutzen), auch Windows-Programme können verwendet werden, stets aktuell, umfangreich (ca. 30 000 Programme sind "für lau" enthalten) - und kostenlos :-)

Habe mir mit dem Wechsel von Windows XP

:-D

auf Ubuntu selbst ein Weihnachtsgeschenk gemacht!

Liebe Grüße

---

Hello again Brucy

Das ist ein schönes Weihnachtsgeschenk.

Ich kenne mich mit Linux gut aus, hatte schon verschiedene Distributionen ausprobiert, als ich noch eine größere Festplatte hatte. Irgendwann bin ich auf eine SSD umgestiegen und weil die so teuer waren, konnte ich mir nur eine 60 GB SSD leisten. Dafür fehlt jetzt der Platz für Linux.

---

Hi gorgar,

Du hast allerdings auch die Möglichkeit, Dir Ubuntu zu brennen oder auf einen USB-Stick zu ziehen und dann von der DVD oder vom Stick Ubuntu zu starten, ohne es zu installieren!

Klasse fand ich

http://www.chip.de/downloads/UNetbootin_34673960.html

---

Stimmt!

Dabei fällt mir ein, damit hatte ich auch mal rumexperimentiert.

Answer 2

 

f(x) = x + 3*e^{-x^2}

lautet die Funktion.

Wenn wir 5 Streifen nehmen, um den Flächeninhalt zu approximieren, sieht es in etwa so aus:

 

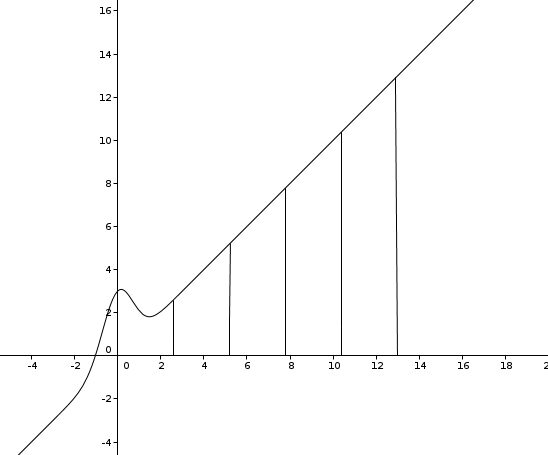
Die Breite eines jeden Streifens ist 13/5 = 2,6

Die Höhe eines jeden Streifens wird berechnet als

(Höhe an linker Grenze des Streifens + Höhe an rechter Grenze des Streifens) / 2

 

1. Streifen:

f(0) = 0 + 3 * e^-0² = 3

f(2,6) = 2,6 + 3 * e^-6,76 ≈ 2,6034776875

Also Fläche des Streifens ≈

2,6 * (3 + 2,6034776875) / 2 = 7,2845209938

 

2. Streifen:

f(2,6) ≈ 2,6034776875

f(5,2) = 5,2 + 3 * e^-5,2² ≈ 5,2

Also Fläche des Streifens ≈

2,6 * (2,6034776875 + 5,2) / 2 = 10,1445209938

 

3. Streifen:

f(5,2) ≈ 5,2

f(7,8) = 7,8 + 3 * e^-60,84 ≈ 7,8

Fläche des Streifens ≈

2,6 * (5,2 + 7,8) / 2 = 16,9

 

4. Streifen:

f(7,8) ≈ 7,8

f(10,4) ≈ 10,4

Fläche des Streifens ≈

2,6 * (7,8 + 10,4) / 2 = 23,66

 

5. Streifen:

f(10,4) ≈ 10,4

f(13) ≈ 13

Fläche des Streifens ≈

2,6 * (10,4 + 13) / 2 = 30,42

 

Summe der Streifen ≈

7,2845209938 +

10,1445209938 +

16,9 +

23,66 +

30,42 =

88,4090419876

 

Besten Gruß

Comments

Danke sehr ich hätte das alleine nie hinbekommen :) MfG