Lösung einer Gleichung mit Logarithmus

Question

Hallo,

ich stehe gerade bei folgender Aufgabe auf dem Schlauch, wäre super, wenn mir jemand fix weiterhelfen könnte...

Aufgabe:

20.000 = 200 * \( \frac{1-1,025^{n}}{1-1,025} \)

n = ?

Problem/Ansatz:

Irgendwie komme ich mit dem Logarithmus nicht weiter, ich habe immer nur negative Werte, auf denen ich den Logarithmus nicht anwenden kann. Es müsste etwas zwischen 50 und 51 herauskommen (das ist meine Näherungslösung)...

DANKE für Eure Hilfe!

Answer 1

$$  n = \frac{ \ln \left[  1-\frac{20000}{200} (1-1.025) \right] }{ \ln(1.025) } $$

Answer 2

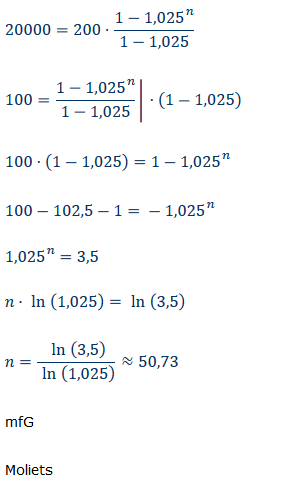
Text erkannt:

\( 20000=200 \cdot \frac{1-1,025^{n}}{1-1,025} \)
\( 100=\frac{1-1,025^{n}}{1-1,025} \mid \cdot(1-1,025) \)
\( 100 \cdot(1-1,025)=1-1,025^{n} \)
\( 100-102,5-1=-1,025^{n} \)
\( 1,025^{n}=3,5 \)
\( n \cdot \ln (1,025)=\ln (3,5) \)
\( n=\frac{\ln (3,5)}{\ln (1,025)} \approx 50,73 \)
\( \mathrm{mfG} \)
Moliets

Answer 3

100*(-0,025)=1-1,025^n

-2,5=1-1,025^n

1,025^n=3,5

n≈50,7343

Ohne Gewähr!

:-)

Comments

\( 1 - 1.025 \ne -0.975 \)

---

Hoppala,

danke für den Hinweis!

:-)

Answer 4

Nachschüssige Rentenendwertformel

En = R·(1 - q^n)/(1 - q)

En/R·(1 - q) = 1 - q^n

q^n = 1 - En/R·(1 - q)

n = LN(1 - En/R·(1 - q)) / LN(q)

Wir setzen mal ein

n = LN(1 - 20000/200·(1 - 1.025)) / LN(1.025) = 50.73432241