Question

Bestimmen Sie die partielle Ableitung ′1(1,2) der Funktion

(1,2)=1^4⋅(x2^4/x2^8+x1^3)

an der Stelle =(1.43; 1.94)

Answer 1

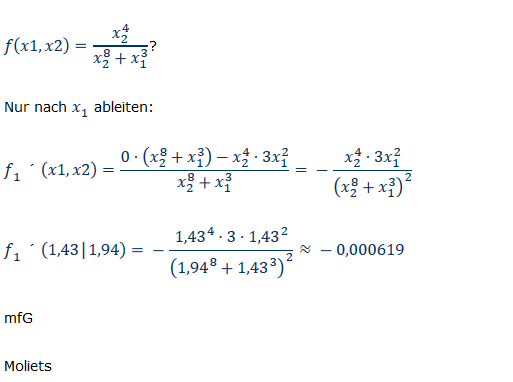
Text erkannt:

\( f(x 1, x 2)=\frac{x_{2}^{4}}{x_{2}^{8}+x_{1}^{3}} ? \)
Nur nach \( x_{1} \) ableiten:
\( f_{1} \cdot(x 1, x 2)=\frac{0 \cdot\left(x_{2}^{8}+x_{1}^{3}\right)-x_{2}^{4} \cdot 3 x_{1}^{2}}{x_{2}^{8}+x_{1}^{3}}=-\frac{x_{2}^{4} \cdot 3 x_{1}^{2}}{\left(x_{2}^{8}+x_{1}^{3}\right)^{2}} \)
\( f_{1} \cdot(1,43 \mid 1,94)=-\frac{1,43^{4} \cdot 3 \cdot 1,43^{2}}{\left(1,94^{8}+1,43^{3}\right)^{2}} \approx-0,000619 \)
\( \mathrm{mfG} \)
Moliets