Aufgabe Bereich Trigonometrie
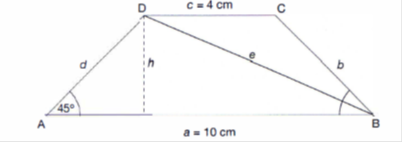
Ein gleichschenkliges Trapez mit der Grundseite a = 10 cm, der Seite
c = 4 cm und den Basiswinkeln von 45° sei gegeben.
Berechnen Sie die Höhe h, die Länge der Seiten b bzw. d, die Länge der Diagonale sowie die Fläche des Trapezes.
Problem/Ansatz:
Geg.: a= 10 cm, c= 4 cm, Winkel 45°
Ges.: h, b, e, A
Ich würde zuerst h ausrechnen. Weiß aber nicht, wie ich den Ansatz hinkriege ?
Würde mich über Unterstützung freuen.
Danke