meines Erachtens ist der p-Wert 14,0 %. Hier meine Rechnung. Basis ist mein Statistik Script, das ich leider in MatheLounge nicht hochladen darf, das du aber jederzeit abrufen kannst, wenn du mir eine Mail schreibst.
Es gilt X ~ N(μ; σ2). σ2 ist bekannt, so dass wir gemäß Seite 155 den Einstichproben-Gaußtest verwenden können, Seite 147. Gegeben ist also:
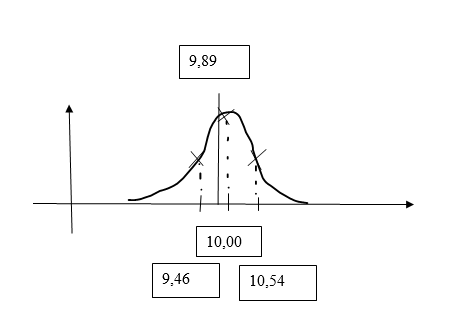
X ~ N(10; 2,29)
σ = 0,54
n = 28
x_quer = 9,89
μ0 = 10
α = 5 %
Bild:
Die Teststatistik ist gemäß S. 147
v = (x_quer-μ0)/σ*\( \sqrt{n} \) = -1,0778 9868
Wir haben hier gemäß Seite 145 einen linksseitigen Test mit
H0: μ ≥ μ0
H1: μ < μ0
In der vorliegenden Aufgabe wird unser H0 als Alternativhypothese H1 bezeichnet.
Rechnung ohne p-Wert:
B = (-∞; -z0,95) = (-∞; -1,6449)
v ∉ B => H0 wird nicht verworfen =>
Die Hypothese, dass der durchschnittliche Umfang der Kugellager im Mittel gleich oder höher als der Sollwert ist, wird *nicht* verworfen.
Rechnung mit p-Wert, Seite 152:
α‘ = Φ(v) = Φ(-1,0778 9868) = 14,05 %
Das ist laut Seite 149 der p-Wert.
p-Wert = 14,05 %
Dies ist der zwischen uns strittige Wert.
α‘ > α => H0 nicht verwerfen lt. Seite 149
Wir kommen zum selben Ergebnis wie bei der Rechnung ohne p-Wert.