Aufgabe:
Das Hyperbelstück H in der x − z−Ebene wird beschrieben durch
\( \mathcal{H}=\left\{(x, y, z) \in \mathbb{R}^{3}: x^{2}-z^{2} / 2=1,-2 \leq z \leq 2, y=0\right\} \)
Volumen bei Rotation um Z-Achse.
Problem/Ansatz:
Es gilt: x = \(\sqrt{1 + \frac{z^2}{2}}\)
miz z=-2 und z=2 habe ich für x, also hier der Radius da y=0 war.
-1 <= x <= \( \sqrt{3} \)
Nun in Zylinderkoordinaten:
x ist gleichzeitig der Radius des Körpers.
0 <= φ <= 2π, da eine ganze Rotation um z
und -2 <= z <= 2
\( \int \limits_{-2}^{2} \int \limits_{0}^{2 \pi} \int \limits_{1}^{\sqrt{3}} r d r d \phi d z \)
nachdem ausrechnen komme ich auf
= 8π
Aber ich denke mein Radius (obere grenze) ist nicht richtig oder?
mfg
Und noch was kleines:
Auf geogebra habe ich das eingeben
x^(2)-((z^(2))/(2))-1=0
und folgendes erhalten
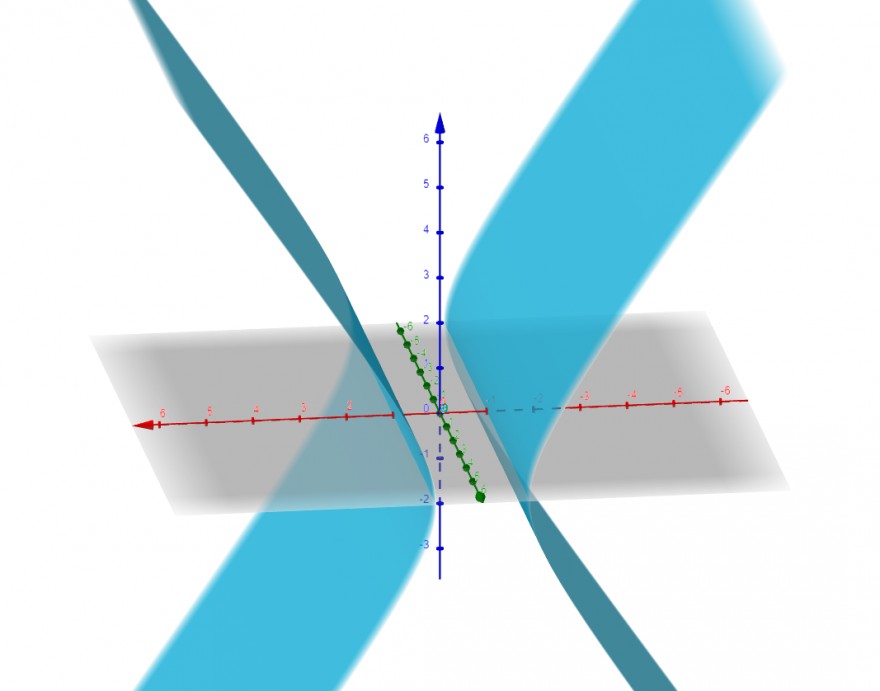
ist das richtig?